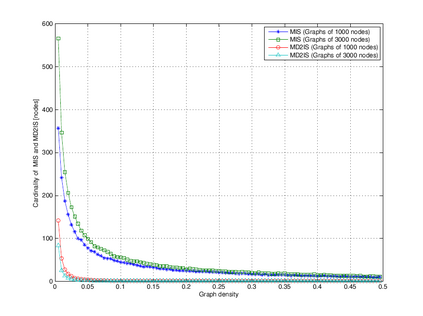
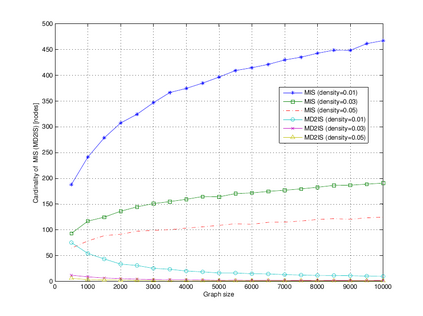
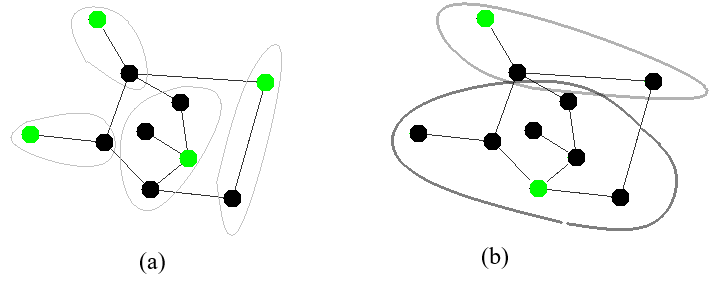
In graph theory, an independent set is a subset of nodes where there are no two adjacent nodes. The independent set is maximal if no node outside the independent set can join it. In network applications, maximal independent sets can be used as cluster heads in ad hoc and wireless sensor networks. In order to deal with any failure in networks, self-stabilizing algorithms have been proposed in the literature to calculate the maximal independent set under different hypotheses. In this paper, we propose a self-stabilizing algorithm to compute a maximal independent set where nodes of the independent set are far from each other at least with distance 3. We prove the correctness and the convergence of the proposed algorithm. Simulation tests show the ability of our algorithm to find a reduced number of nodes in large scale networks which allows strong control of networks
翻译:在图形理论中,独立集是没有两个相邻节点的节点的子集。独立集如果独立集在独立集之外没有节点可以加入它,则是最大节点。在网络应用中,最大独立集可以用作临时和无线传感器网络的集群头。为了处理网络中的任何故障,文献中提出了自我稳定算法,以计算不同假设下的最大独立集。在本文中,我们提议了一种自我稳定算法,以计算一个最大独立集,独立集的节点彼此距离最远,至少距离最远。在网络应用中,我们证明了拟议算法的正确性和趋同性。模拟测试表明我们的算法能够在大型网络中找到数量较少的节点,从而能够对网络进行强有力的控制。