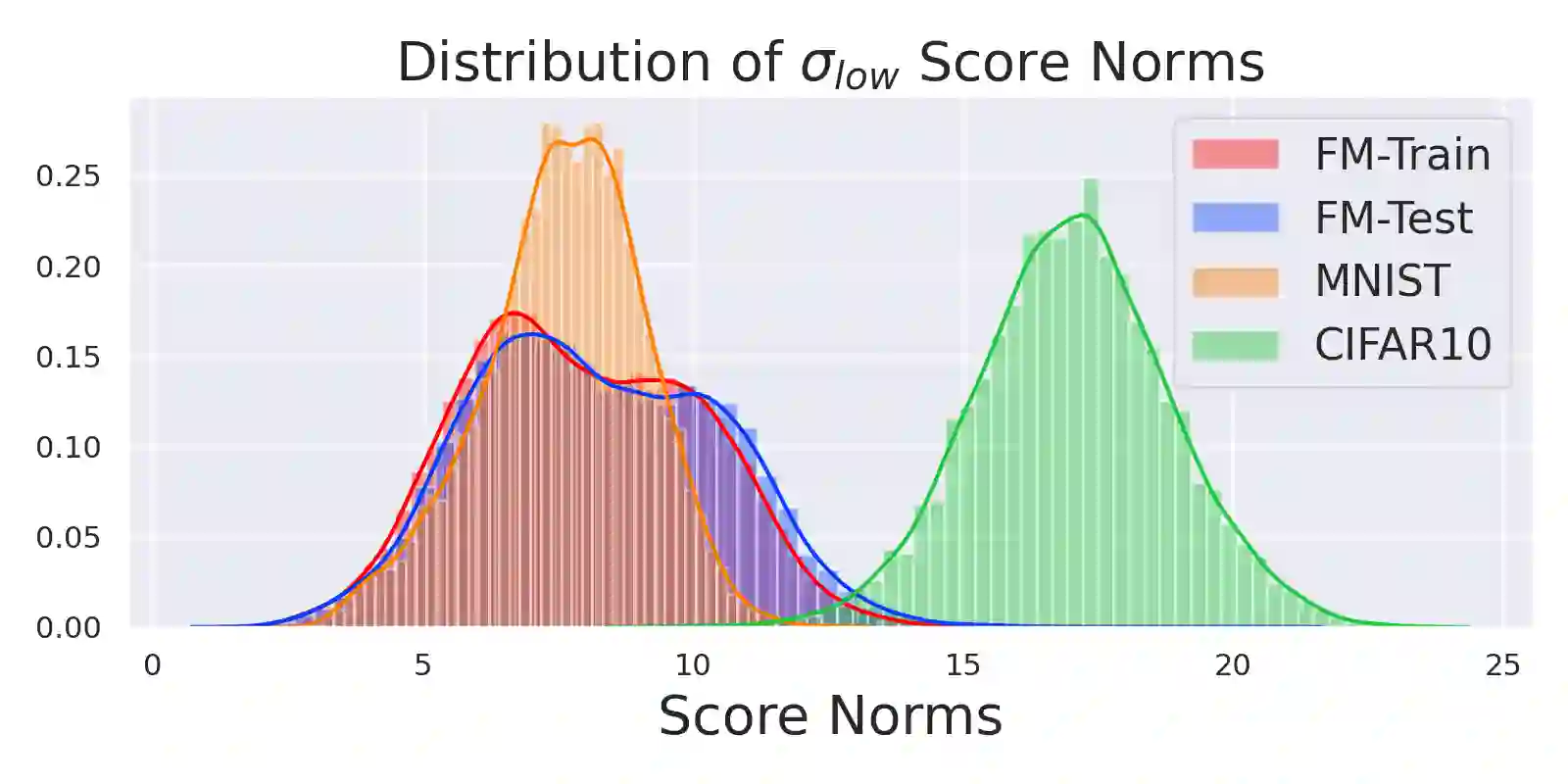
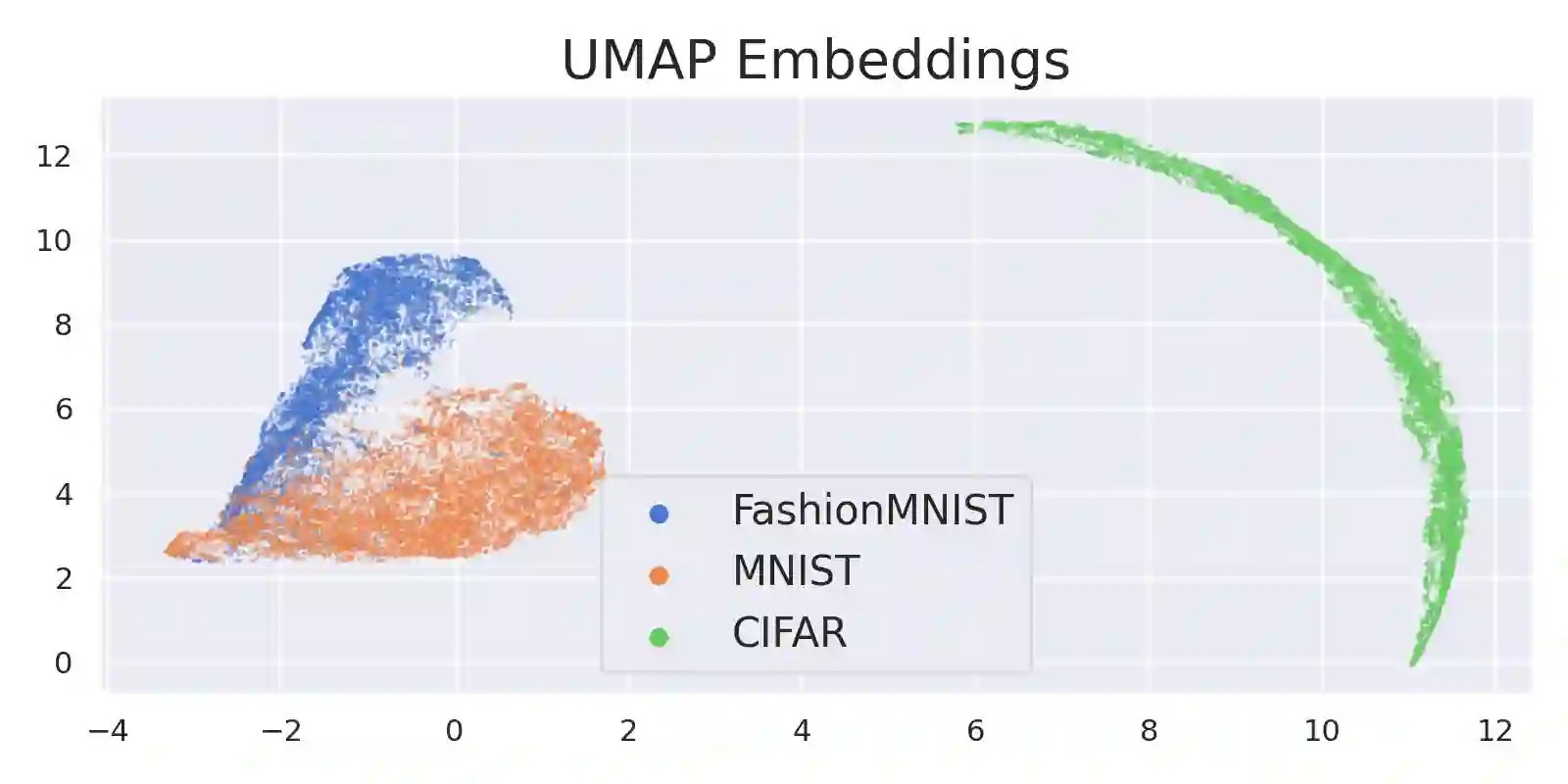
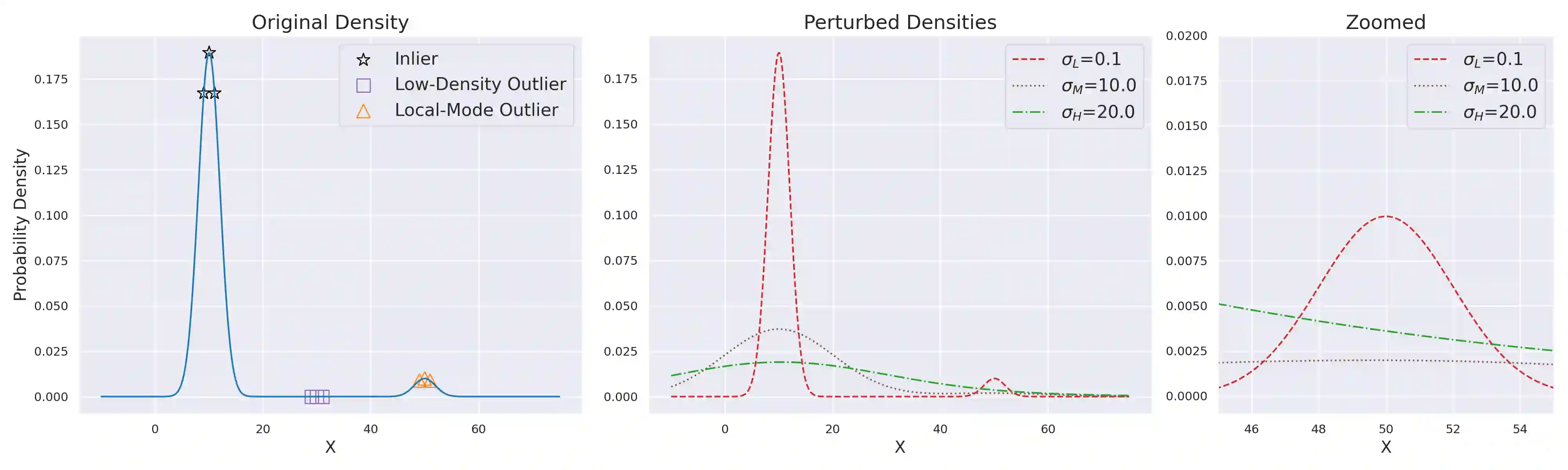
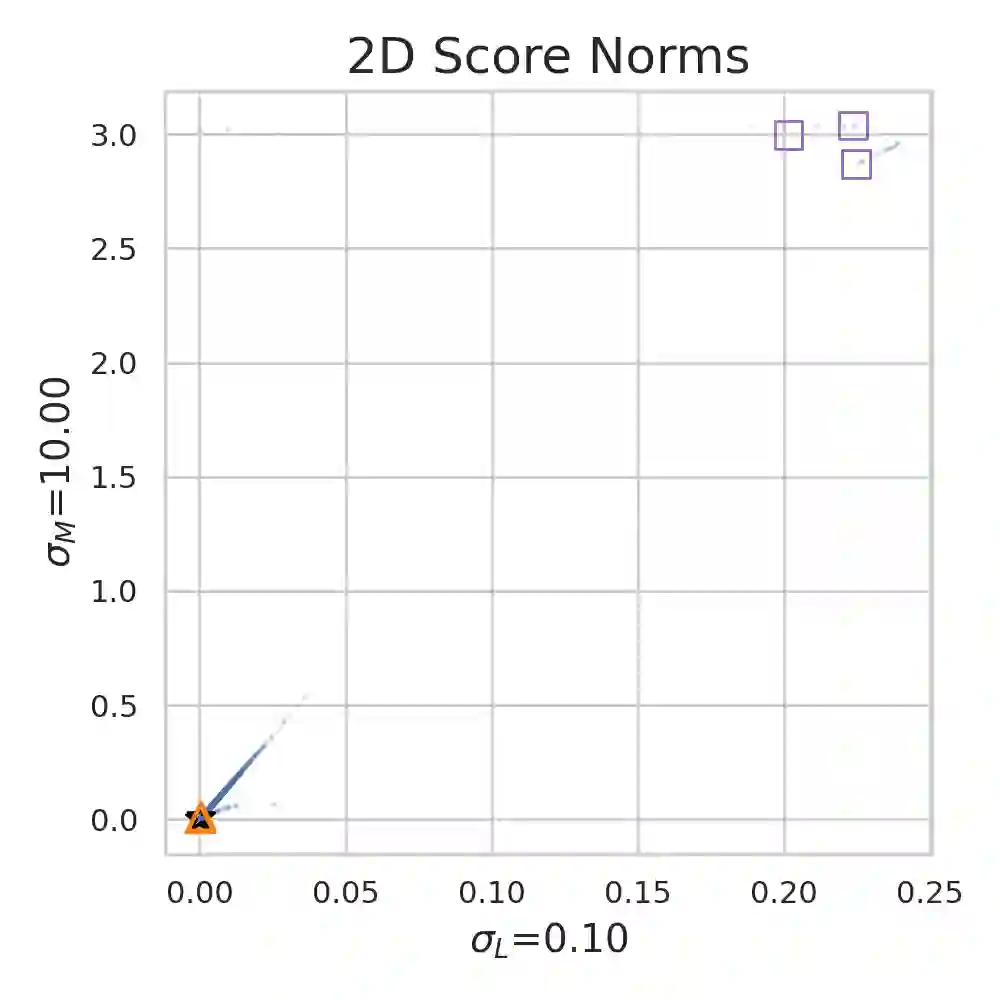
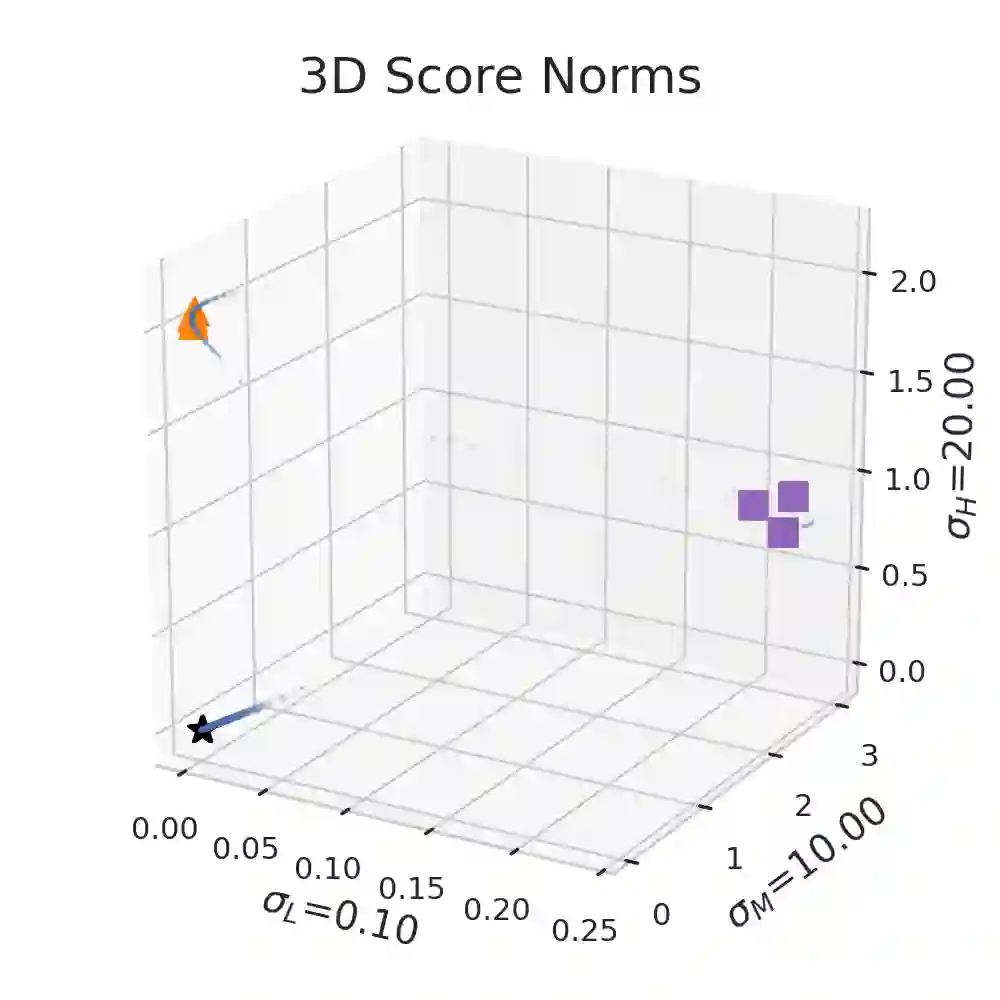
We present a new methodology for detecting out-of-distribution (OOD) images by utilizing norms of the score estimates at multiple noise scales. A score is defined to be the gradient of the log density with respect to the input data. Our methodology is completely unsupervised and follows a straight forward training scheme. First, we train a deep network to estimate scores for levels of noise. Once trained, we calculate the noisy score estimates for N in-distribution samples and take the L2-norms across the input dimensions (resulting in an NxL matrix). Then we train an auxiliary model (such as a Gaussian Mixture Model) to learn the in-distribution spatial regions in this L-dimensional space. This auxiliary model can now be used to identify points that reside outside the learned space. Despite its simplicity, our experiments show that this methodology significantly outperforms the state-of-the-art in detecting out-of-distribution images. For example, our method can effectively separate CIFAR-10 (inlier) and SVHN (OOD) images, a setting which has been previously shown to be difficult for deep likelihood models.
翻译:我们通过在多个噪音尺度上使用分数估计标准来检测分数外(OOD)图像的新方法。 分数的定义是输入数据时的日志密度梯度。 我们的方法完全无人监督,并遵循直线前方培训计划。 首先, 我们训练一个深网络来估计噪音等级的分数。 我们经过培训后, 我们计算出N分布样本的噪音分数估计数, 并在输入维度( 产生NxL 矩阵中) 中取出L2- norms 。 然后, 我们训练了一个辅助模型( 如高斯混合模型) 来学习这个L- 维度空间的分布空间区域。 这个辅助模型现在可以用来确定位于所学空间之外的点。 尽管很简洁, 我们的实验显示, 这个方法大大超出了探测分数图像的状态。 例如, 我们的方法可以有效地将CIFAR- 10 (inlier) 和 SVHN (ODD) 图像区分开来, 以前已经为极难进行深可能性模型的设置 。