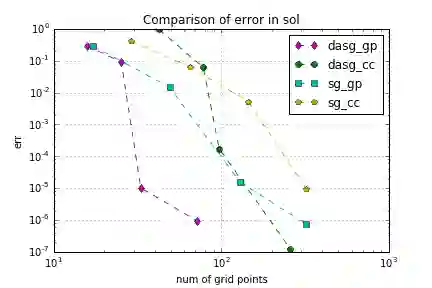
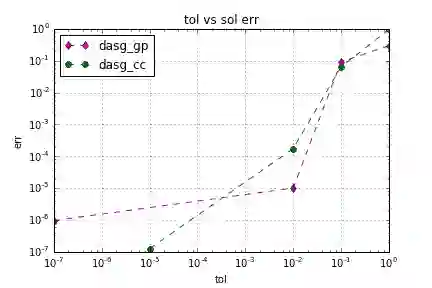
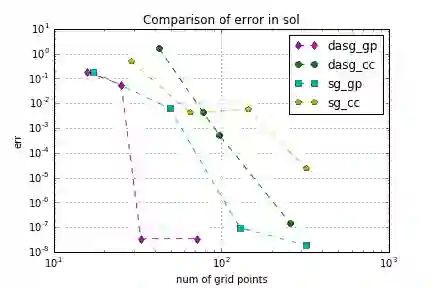
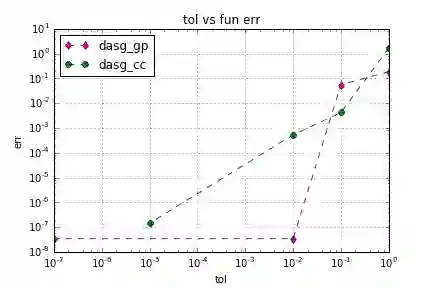
Stochastic optimisation problems minimise expectations of random cost functions. We use 'optimise then discretise' method to solve stochastic optimisation. In our approach, accurate quadrature methods are required to calculate the objective, gradient or Hessian which are in fact integrals. We apply the dimension-adaptive sparse grid quadrature to approximate these integrals when the problem is high dimensional. Dimension-adaptive sparse grid quadrature shows high accuracy and efficiency in computing an integral with a smooth integrand. It is a kind of generalisation of the classical sparse grid method, which refines different dimensions according to their importance. We show that the dimension-adaptive sparse grid quadrature has better performance in the optimise then discretise' method than the 'discretise then optimise' method.
翻译:托盘优化问题将随机成本函数的预期最小化。 我们使用“ 优化然后分解” 方法来解决随机优化问题。 在我们的方法中, 需要精确的二次曲线方法来计算目标、 梯度或者事实上是整体的赫西恩 。 当问题为高维时, 我们应用维度适应性稀有网格二次曲线来接近这些整体。 维度适应性稀有网格二次曲线在计算一个带有光滑整形的构件时表现出很高的准确性和效率。 这是典型的稀有网格方法的一种一般化方法, 它根据它们的重要性来细化不同的维度。 我们显示, 维度适应性稀有网格二次曲线二次曲线的二次曲线比“ 分解后优化” 方法的性要好。