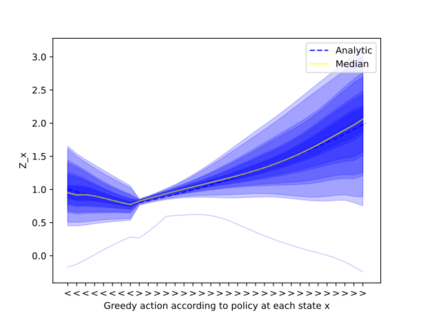
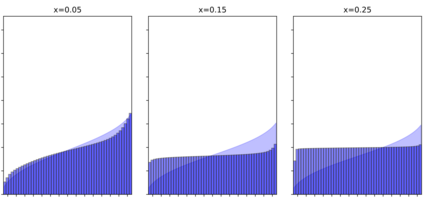
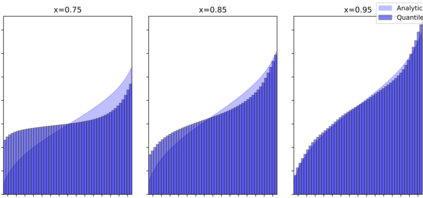
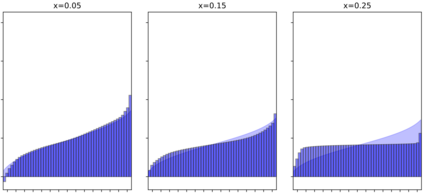
Continuous-time reinforcement learning offers an appealing formalism for describing control problems in which the passage of time is not naturally divided into discrete increments. Here we consider the problem of predicting the distribution of returns obtained by an agent interacting in a continuous-time, stochastic environment. Accurate return predictions have proven useful for determining optimal policies for risk-sensitive control, learning state representations, multiagent coordination, and more. We begin by establishing the distributional analogue of the Hamilton-Jacobi-Bellman (HJB) equation for It\^o diffusions and the broader class of Feller-Dynkin processes. We then specialize this equation to the setting in which the return distribution is approximated by $N$ uniformly-weighted particles, a common design choice in distributional algorithms. Our derivation highlights additional terms due to statistical diffusivity which arise from the proper handling of distributions in the continuous-time setting. Based on this, we propose a tractable algorithm for approximately solving the distributional HJB based on a JKO scheme, which can be implemented in an online control algorithm. We demonstrate the effectiveness of such an algorithm in a synthetic control problem.
翻译:连续时间强化学习为描述时间的流逝并非自然地分为离散增量的控制问题提供了一种颇具吸引力的形式主义。 这里我们考虑的是预测在连续时间、随机环境中相互作用的代理人获得的回报分布的问题。 准确的返回预测已证明对确定风险敏感控制的最佳政策、 学习国家表现、 多剂协调等都是有益的。 我们首先通过建立HJB(HJB)对It ⁇ o扩散和Feller-Dynkin进程大类分配的分布性模拟方程式(HJB)开始为It ⁇ o扩散和Feller-Dynkin进程进行分布性模拟。 我们然后将这一方程式专门化为返回分布近似于美元统一加权粒子的环境,这是分配算法中的一种通用设计选择。 我们的推算结果突出了由于在连续时间设置中正确处理分配所产生的统计差异性而产生的额外条件。 基于这一点,我们提出一种可移动的算法,以大致解决基于JKO计划的分配性HJB(可在网上控制算法中实施)的分布性 HJK。 我们展示了这种合成控制算法的有效性。