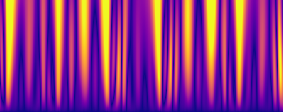
We present a data-driven approach to learning surrogate models for amplitude equations, and illustrate its application to interfacial dynamics of phase field systems. In particular, we demonstrate learning effective partial differential equations describing the evolution of phase field interfaces from full phase field data. We illustrate this on a model phase field system, where analytical approximate equations for the dynamics of the phase field interface (a higher order eikonal equation and its approximation, the Kardar-Parisi-Zhang (KPZ) equation) are known. For this system, we discuss data-driven approaches for the identification of equations that accurately describe the front interface dynamics. When the analytical approximate models mentioned above become inaccurate, as we move beyond the region of validity of the underlying assumptions, the data-driven equations outperform them. In these regimes, going beyond black-box identification, we explore different approaches to learn data-driven corrections to the analytically approximate models, leading to effective gray box partial differential equations.
翻译:我们提出了一个数据驱动方法,用于学习振幅方程式的替代模型,并演示其在相位字段系统间动态中的应用。特别是,我们展示了从整个相位字段数据中描述相位字段界面演变过程的有效的部分差异方程式。我们用一个模型阶段字段系统来说明这一点,在这个系统中,对相位字段界面动态的分析近似方程式(一个更高的等式及其近似式,Kardar-Parisi-Zhang(KPZ)等式)是已知的。对于这个系统,我们讨论了数据驱动方法,用以识别准确描述前位界面动态的方程式。当上述分析近似方程式变得不准确时,当我们超越基本假设的有效性区域时,数据驱动方程式就超越了这些方程式。在这些系统中,我们除了黑箱识别之外,还探索了不同的方法来学习数据驱动对分析近度模型的校正,从而导致有效的灰盒部分差异方程式。