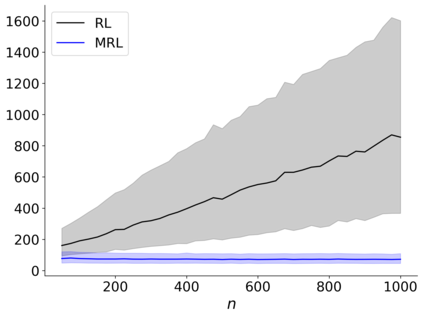
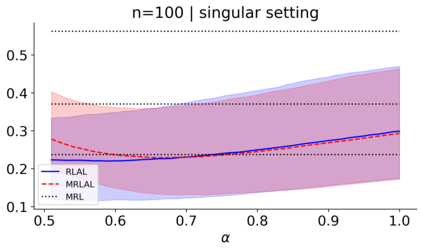
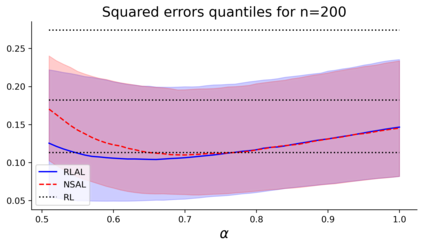
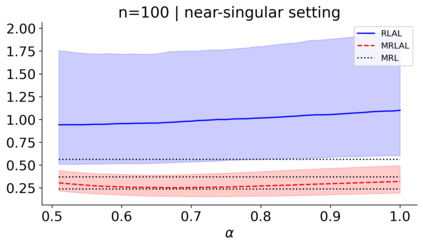
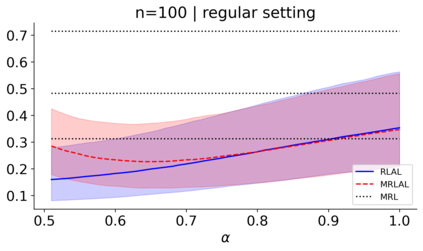
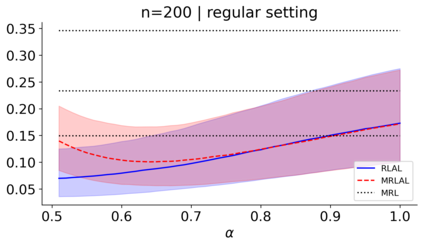
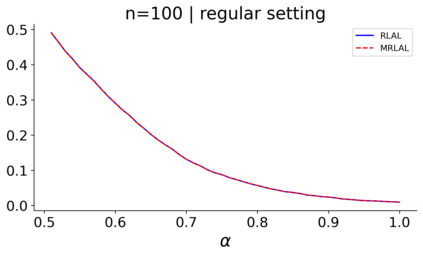
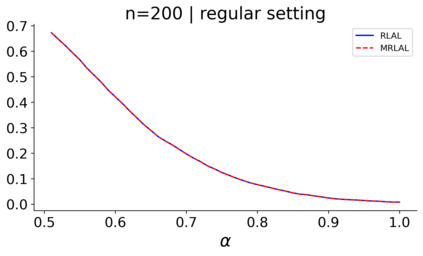
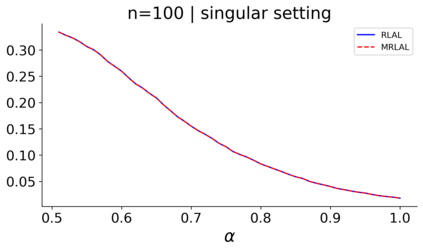
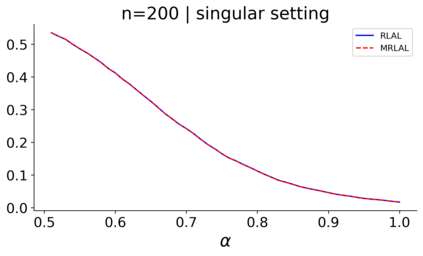
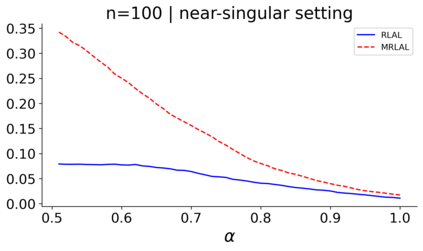
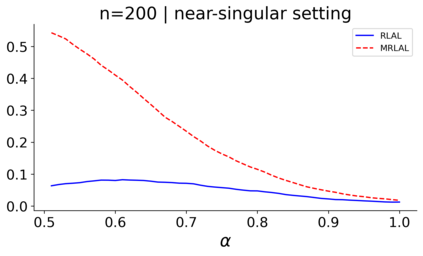
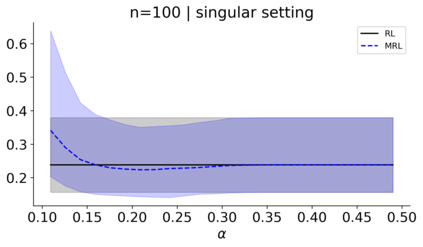
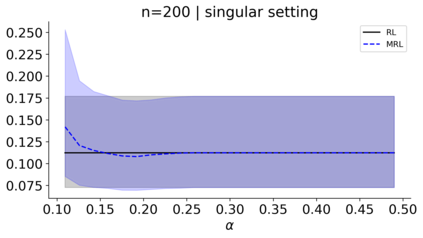
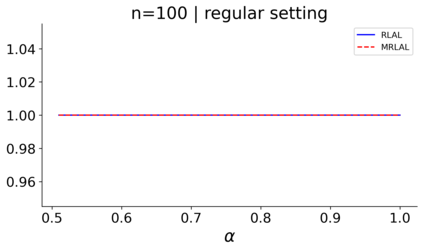
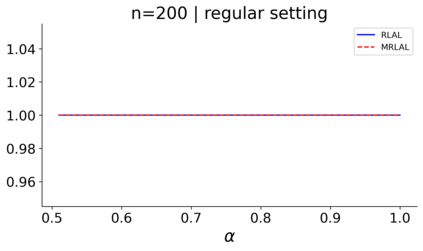
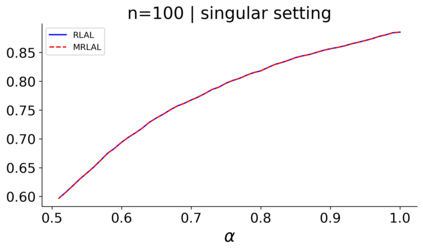
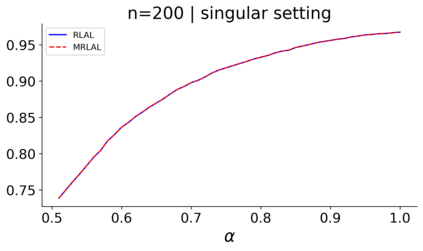
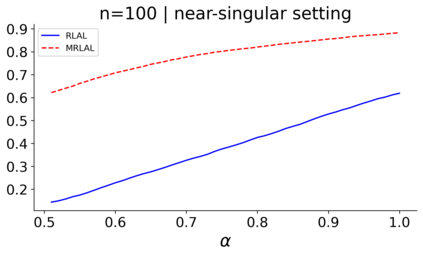
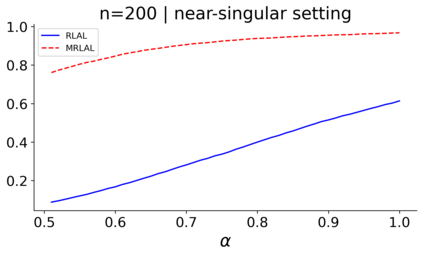
We build a unifying convex analysis framework characterizing the statistical properties of a large class of penalized estimators, both under a regular and an irregular design. Our framework interprets penalized estimators as proximal estimators, defined by a proximal operator applied to a corresponding initial estimator. We characterize the asymptotic properties of proximal estimators, showing that their asymptotic distribution follows a closed-form formula depending only on (i) the asymptotic distribution of the initial estimator, (ii) the estimator's limit penalty subgradient and (iii) the inner product defining the associated proximal operator. In parallel, we characterize the Oracle features of proximal estimators from the properties of their penalty's subgradients. We exploit our approach to systematically cover linear regression settings with a regular or irregular design. For these settings, we build new $\sqrt{n}-$consistent, asymptotically normal Ridgeless-type proximal estimators, which feature the Oracle property and are shown to perform satisfactorily in practically relevant Monte Carlo settings.
翻译:我们构建了一个统一的曲线分析框架, 描述在常规和非常规设计下一大批受罚估量的统计属性。 我们的框架将受罚估量解释为准度估量值, 由准运算人定义, 适用于相应的初始估量仪。 我们用一个定期或非常规设计来描述准度估量器的无症状特性, 显示其无症状分布遵循一个封闭式公式, 仅取决于( 一) 初始估量器的无症状分布, (二) 估量器的限值亚梯度和(三) 定义相关准度操作者的内产产品。 与此同时, 我们从其次梯度属性中确定准度估量器的奥克拉特特性。 我们利用我们的方法, 系统覆盖定期或非常规设计的线性回归设置。 对于这些环境, 我们新建了一个新的 $\ qrt{nt{n}- $ conformative 公式, 随机正常的脊脊椎定型估量器, 将自动显示为“ 色” 。