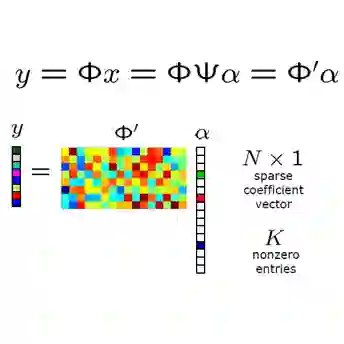
Sampling strategies are important for sparse imaging methodologies, especially those employing the discrete Fourier transform (DFT). Chaotic sensing is one such methodology that employs deterministic, fractal sampling in conjunction with finite, iterative reconstruction schemes to form an image from limited samples. Using a sampling pattern constructed entirely from periodic lines in DFT space, chaotic sensing was found to outperform traditional compressed sensing for magnetic resonance imaging; however, only one such sampling pattern was presented and the reason for its fractal nature was not proven. Through the introduction of a novel image transform known as the kaleidoscope transform, which formalises and extends upon the concept of downsampling and concatenating an image with itself, this paper: (1) demonstrates a fundamental relationship between multiplication in modular arithmetic and downsampling; (2) provides a rigorous mathematical explanation for the fractal nature of the sampling pattern in the DFT; and (3) leverages this understanding to develop a collection of novel fractal sampling patterns for the 2D DFT with customisable properties. The ability to design tailor-made fractal sampling patterns expands the utility of the DFT in chaotic imaging and may form the basis for a bespoke chaotic sensing methodology, in which the fractal sampling matches the imaging task for improved reconstruction.
翻译:取样战略对稀有成像方法十分重要,特别是对于使用离散的Fourier变形(DFT)的成像方法十分重要。 采集遥感是使用确定性分层取样的方法之一,它与有限的迭代重建计划一起采用固定的分层取样方法,从有限的样品中形成图像。使用完全从DFT空间的定期线上建成的抽样模式,发现混乱的遥感方法优于传统的磁共振成像压缩感光成像法;然而,只展示了一种这种抽样模式,其分形性质的原因没有得到证明。通过引进一种新型图像变形,称为Kaleidoscope变形法,这种变形法在降色和将图像与自己搭配的概念上形成正规化和扩展。 本文:(1) 展示了模块计算和降影的倍化之间的基本关系;(2) 对DFTFT的采样模式的分流性质提供了严格的数学解释;(3) 利用这种理解,为2DFT的成形特性开发新的分形抽样采样模式,这种变形模型将形成正规的成形图,从而扩大FTFSimimmamamas的图像的利用。