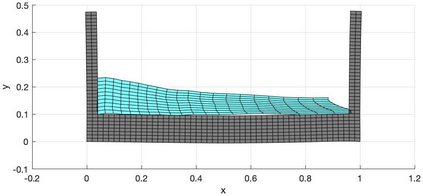
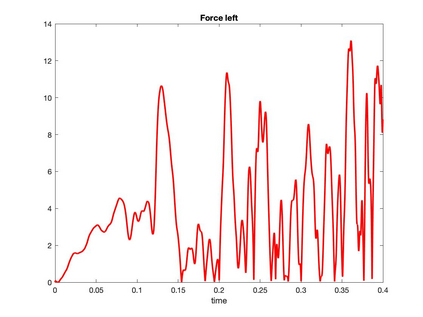
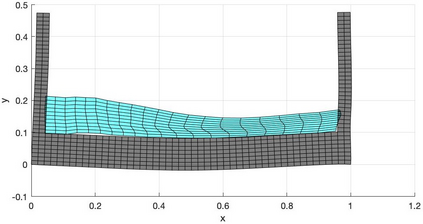
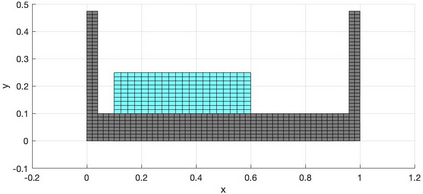
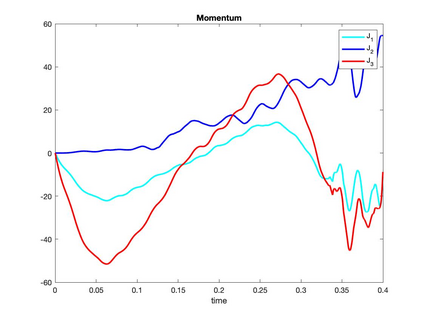
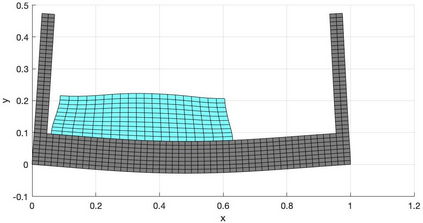
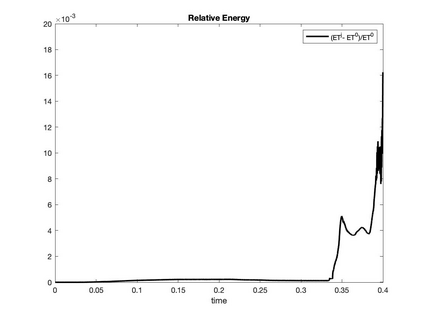
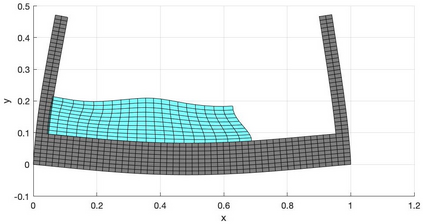
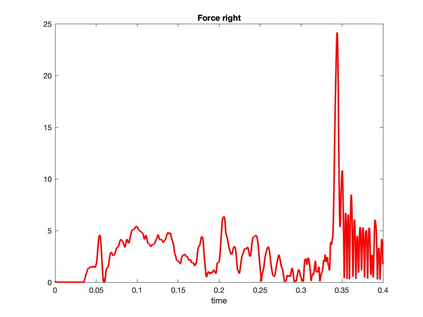
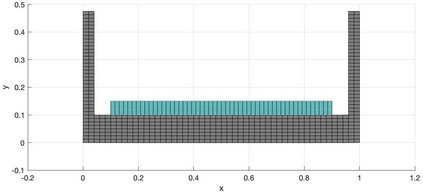
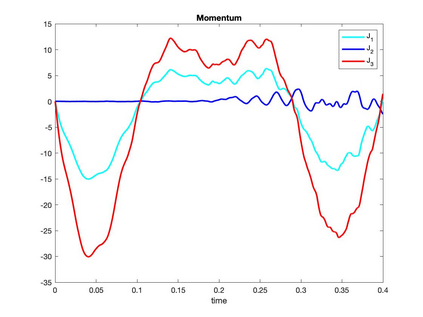
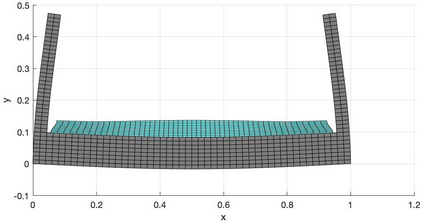
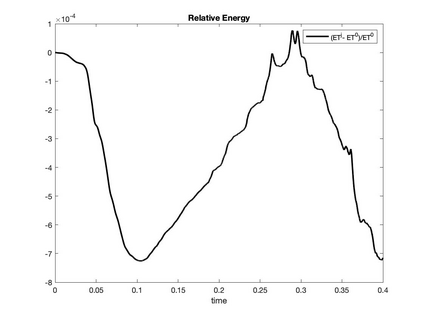
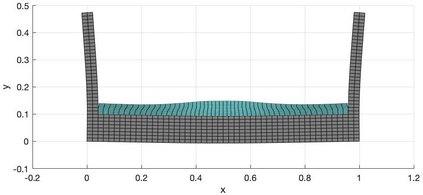
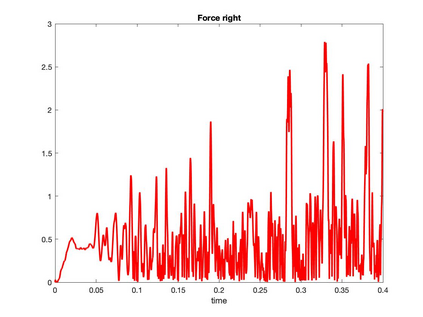
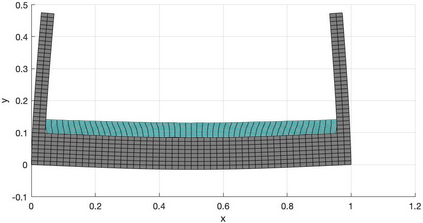
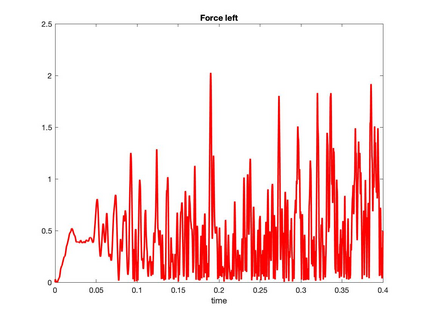
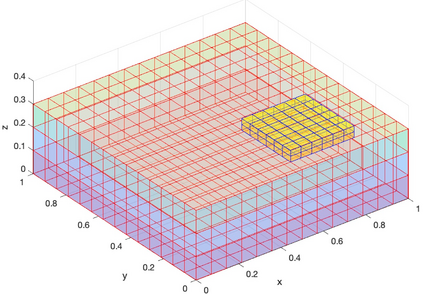
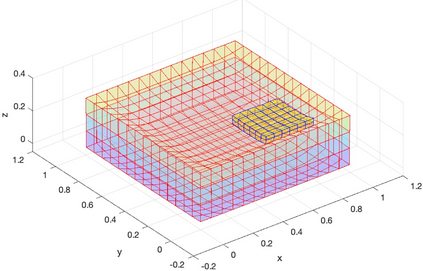
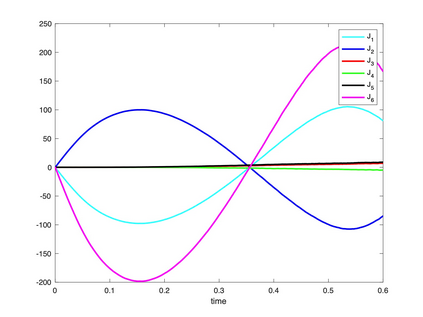
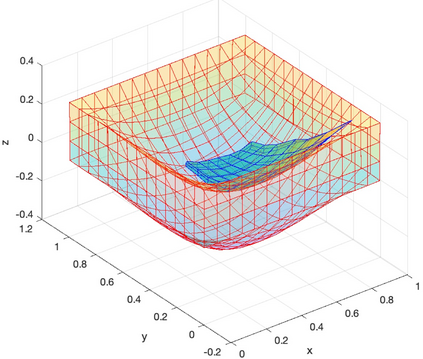
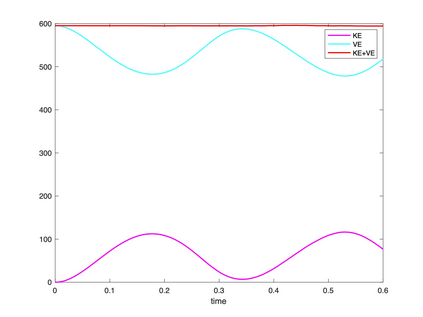
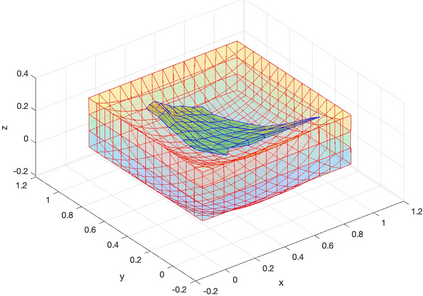
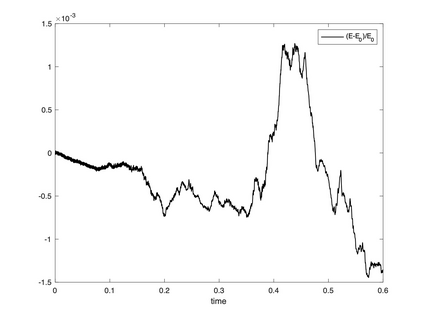
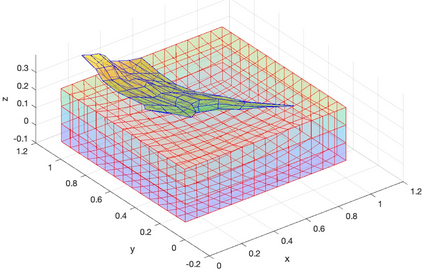
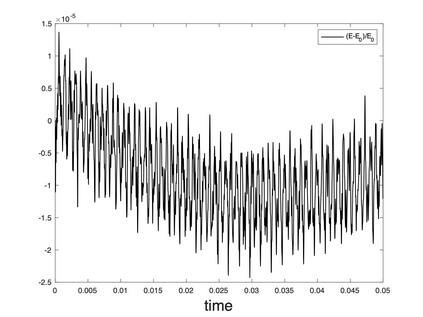
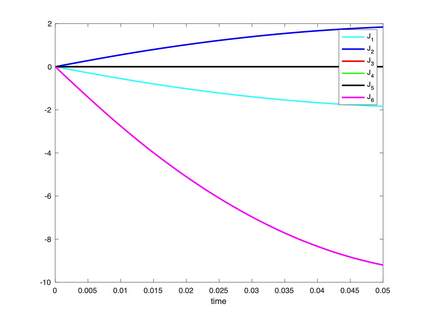
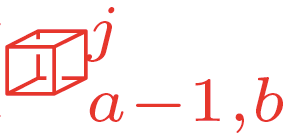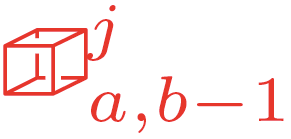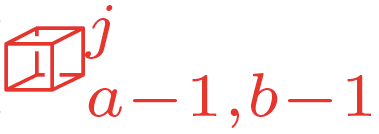We present a geometric variational discretization of nonlinear elasticity in 2D and 3D in the Lagrangian description. A main step in our construction is the definition of discrete deformation gradients and discrete Cauchy-Green deformation tensors, which allows for the development of a general discrete geometric setting for frame indifferent isotropic hyperelastic models. The resulting discrete framework is in perfect adequacy with the multisymplectic discretization of fluids proposed earlier by the authors. Thanks to the unified discrete setting, a geometric variational discretization can be developed for the coupled dynamics of a fluid impacting and flowing on the surface of an hyperelastic body. The variational treatment allows for a natural inclusion of incompressibility and impenetrability constraints via appropriate penalty terms. We test the resulting integrators in 2D and 3D with the case of a barotropic fluid flowing on incompressible rubber-like nonlinear models.
翻译:在Lagrangian 描述中,我们在2D 和 3D 描述中提出了非线性弹性的几何差异分解。我们构建过程中的一个主要步骤是定义离散变形梯度和离散孔-绿色变异变色器,这样就可以为无偏差的等离式超弹性模型开发出一个普通离散几何设置。由此产生的离散框架与作者早先提议的液体多视离异化非常合适。由于统一的离散设置,可以开发出一个几何变异分解,以结合流体在超弹性体表面影响和流动的动态。变异处理使得可以通过适当的惩罚条件自然地纳入不压缩和不易变异性制约。我们用压压性橡胶非线性模型上流的巴色流体试验2D 和 3D 。