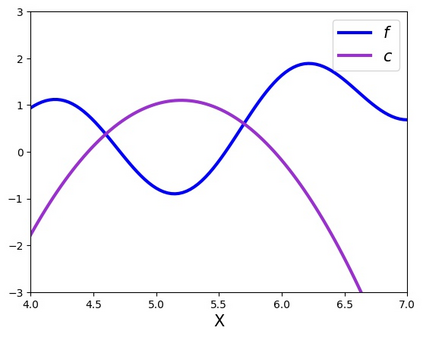
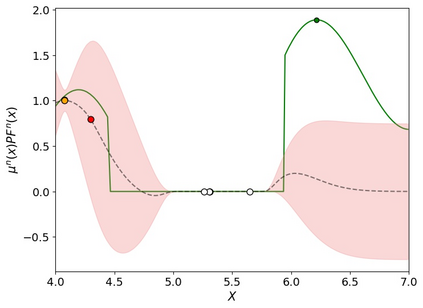
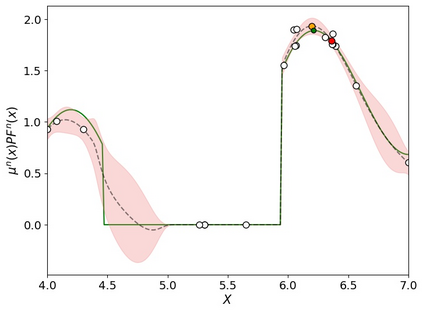
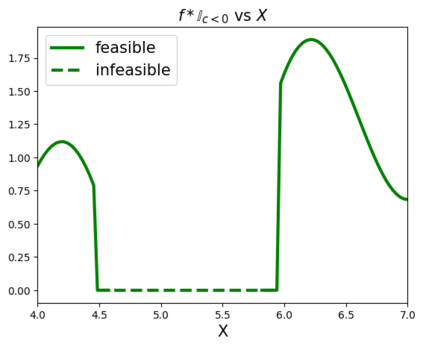
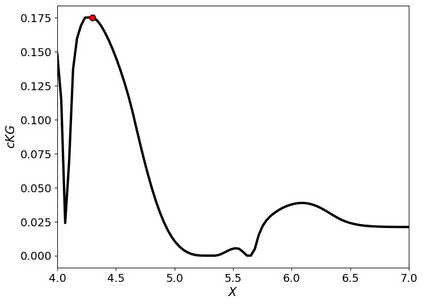
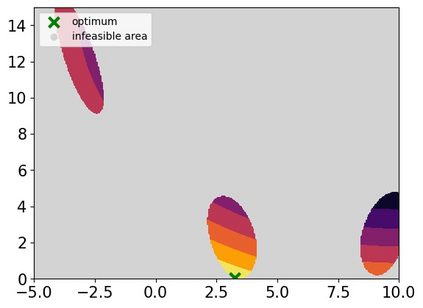
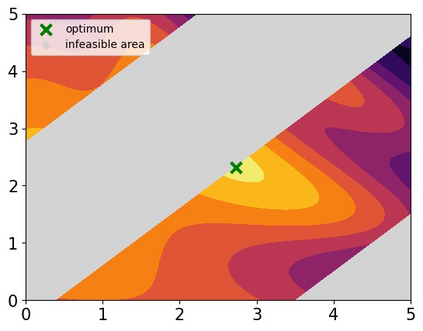
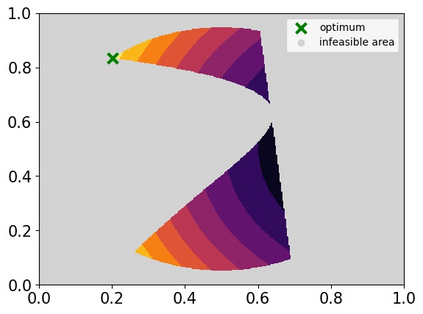
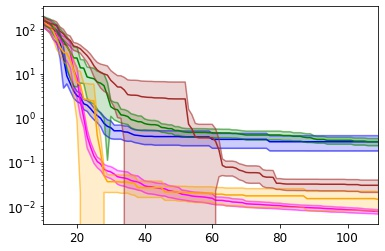
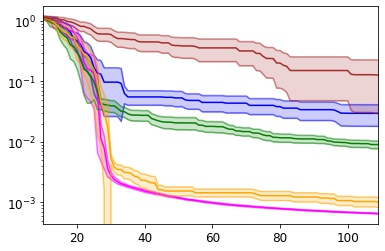
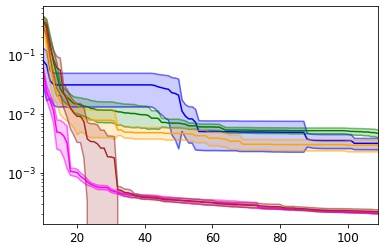
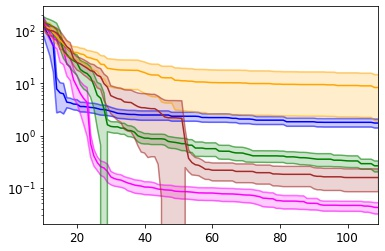
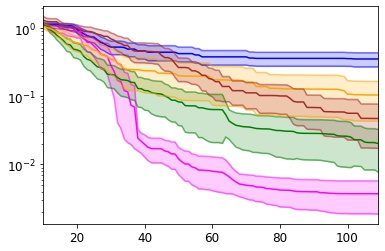
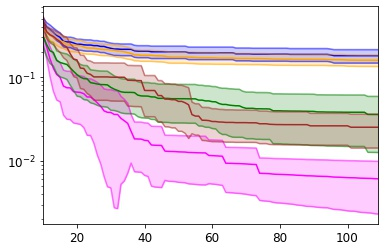
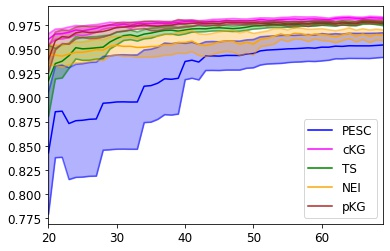
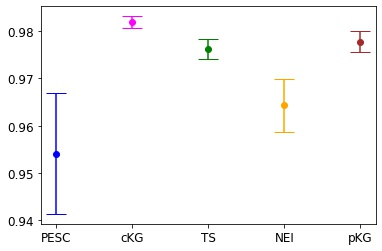
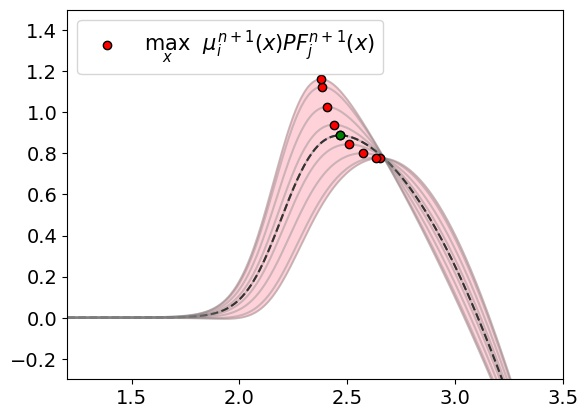
Many real-world optimisation problems such as hyperparameter tuning in machine learning or simulation-based optimisation can be formulated as expensive-to-evaluate black-box functions. A popular approach to tackle such problems is Bayesian optimisation (BO), which builds a response surface model based on the data collected so far, and uses the mean and uncertainty predicted by the model to decide what information to collect next. In this paper, we propose a novel variant of the well-known Knowledge Gradient acquisition function that allows it to handle constraints. We empirically compare the new algorithm with four other state-of-the-art constrained Bayesian optimisation algorithms and demonstrate its superior performance. We also prove theoretical convergence in the infinite budget limit.
翻译:许多现实世界的优化问题,如机器学习或模拟优化的超参数调试等,可以被设计成昂贵到评估黑盒功能。一种解决这类问题的流行方法就是巴伊西亚优化(BO),它根据迄今收集的数据建立了一个反应表面模型,并使用模型预测的平均值和不确定性来决定下一步要收集的信息。在本文中,我们提出了一个众所周知的知识进步获取功能的新变体,使其能够处理各种限制。我们用经验将新的算法与其他四种最先进的巴伊西亚受限制的优化算法进行比较,并展示其优异性。我们还证明了在无限预算限制方面的理论趋同。