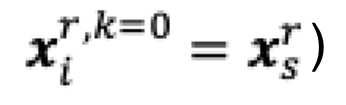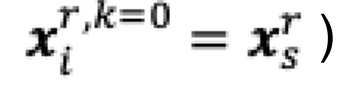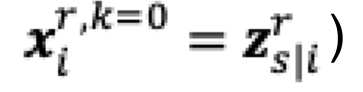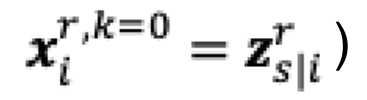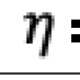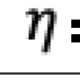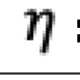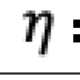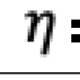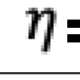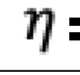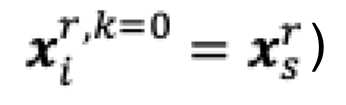The primal-dual method of multipliers (PDMM) was originally designed for solving a decomposable optimisation problem over a general network. In this paper, we revisit PDMM for optimisation over a centralized network. We first note that the recently proposed method FedSplit [1] implements PDMM for a centralized network. In [1], Inexact FedSplit (i.e., gradient based FedSplit) was also studied both empirically and theoretically. We identify the cause for the poor reported performance of Inexact FedSplit, which is due to the improper initialisation in the gradient operations at the client side. To fix the issue of Inexact FedSplit, we propose two versions of Inexact PDMM, which are referred to as gradient-based PDMM (GPDMM) and accelerated GPDMM (AGPDMM), respectively. AGPDMM accelerates GPDMM at the cost of transmitting two times the number of parameters from the server to each client per iteration compared to GPDMM. We provide a new convergence bound for GPDMM for a class of convex optimisation problems. Our new bounds are tighter than those derived for Inexact FedSplit. We also investigate the update expressions of AGPDMM and SCAFFOLD to find their similarities. It is found that when the number K of gradient steps at the client side per iteration is K=1, both AGPDMM and SCAFFOLD reduce to vanilla gradient descent with proper parameter setup. Experimental results indicate that AGPDMM converges faster than SCAFFOLD when K>1 while GPDMM converges slightly worse than SCAFFOLD.
翻译:基本乘数法( PDMM ) 最初设计用于解决整个网络中可分解的最佳化问题的初始方法( PDMM ) 。 在本文中, 我们重新审视 PDMM, 以便在集中网络中实现优化。 我们首先注意到, 最近提议的 FedSplit [1] 方法在中央网络中实施 PDM MD PD MM 。 在 [1] 中, 还从经验上和理论上研究了不Exact FedSplit (即基于梯度的 FedSplit) 。 我们找出了由于客户端梯度操作初始化不当, 导致不合规的 FedSpllit 表现不佳的原因。 为了解决不合规化的 PDMMD 问题, 我们提出了两种版本的Inexact PDMMD PD PDM 方法, 分别称为基于梯度的 PDMMM (GDMMM) 和加速的 GPDMMMM (A) (A), 其服务器向每个客户发送的参数数量比GPDMDMD 的参数要高出两倍。 我们为GPDMDMD mD 的递解的递增缩算的客户级的递增缩算的缩算法, 当我们公司在更精化时, 的递解的客户端的递解的递解的递缩时, 时, 时, 的递减了KDMDFDFDFDFDFDFDFDFDFDFDFDLDDDDDDFDFDD 。