Classification of Radiologically Isolated Syndrome and Clinically Isolated Syndrome with Machine-Learning Techniques

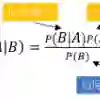
Background and purpose: The unanticipated detection by magnetic resonance imaging (MRI) in the brain of asymptomatic subjects of white matter lesions suggestive of multiple sclerosis (MS) has been named radiologically isolated syndrome (RIS). As the difference between early MS [i.e. clinically isolated syndrome (CIS)] and RIS is the occurrence of a clinical event, it is logical to improve detection of the subclinical form without interfering with MRI as there are radiological diagnostic criteria for that. Our objective was to use machine-learning classification methods to identify morphometric measures that help to discriminate patients with RIS from those with CIS. Methods: We used a multimodal 3-T MRI approach by combining MRI biomarkers (cortical thickness, cortical and subcortical grey matter volume, and white matter integrity) of a cohort of 17 patients with RIS and 17 patients with CIS for single-subject level classification. Results: The best proposed models to predict the diagnosis of CIS and RIS were based on the Naive Bayes, Bagging and Multilayer Perceptron classifiers using only three features: the left rostral middle frontal gyrus volume and the fractional anisotropy values in the right amygdala and right lingual gyrus. The Naive Bayes obtained the highest accuracy [overall classification, 0.765; area under the receiver operating characteristic (AUROC), 0.782]. Conclusions: A machine-learning approach applied to multimodal MRI data may differentiate between the earliest clinical expressions of MS (CIS and RIS) with an accuracy of 78%. Keywords: Bagging; Multilayer Perceptron; Naive Bayes classifier; clinically isolated syndrome; diffusion tensor imaging; machine-learning; magnetic resonance imaging; multiple sclerosis; radiologically isolated syndrome.