Interpretable and Compositional Relation Learning by Joint Training with an Autoencoder

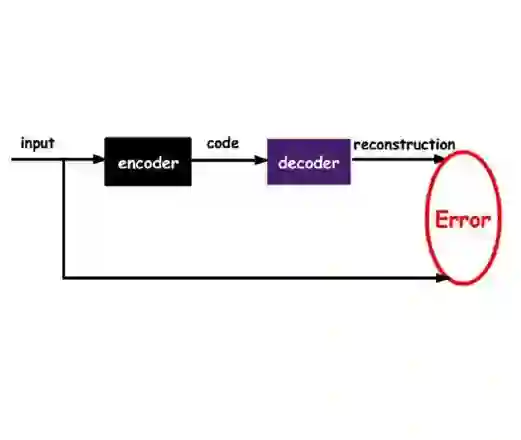
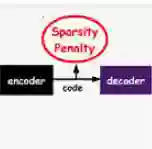
Embedding models for entities and relations are extremely useful for recovering missing facts in a knowledge base. Intuitively, a relation can be modeled by a matrix mapping entity vectors. However, relations reside on low dimension sub-manifolds in the parameter space of arbitrary matrices---for one reason, composition of two relations $\boldsymbol{M}_1,\boldsymbol{M}_2$ may match a third $\boldsymbol{M}_3$ (e.g. composition of relations currency_of_country and country_of_film usually matches currency_of_film_budget), which imposes compositional constraints to be satisfied by the parameters (i.e. $\boldsymbol{M}_1\cdot \boldsymbol{M}_2\approx \boldsymbol{M}_3$). In this paper we investigate a dimension reduction technique by training relations jointly with an autoencoder, which is expected to better capture compositional constraints. We achieve state-of-the-art on Knowledge Base Completion tasks with strongly improved Mean Rank, and show that joint training with an autoencoder leads to interpretable sparse codings of relations, helps discovering compositional constraints and benefits from compositional training. Our source code is released at github.com/tianran/glimvec.