Study of a structure preserving finite volume scheme for a nonlocal cross-diffusion system

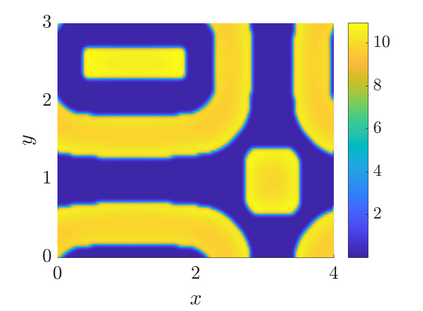
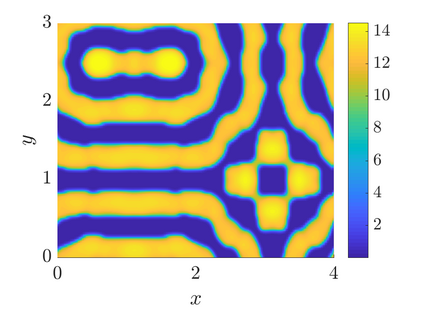
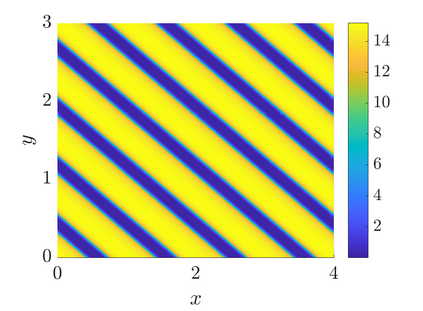
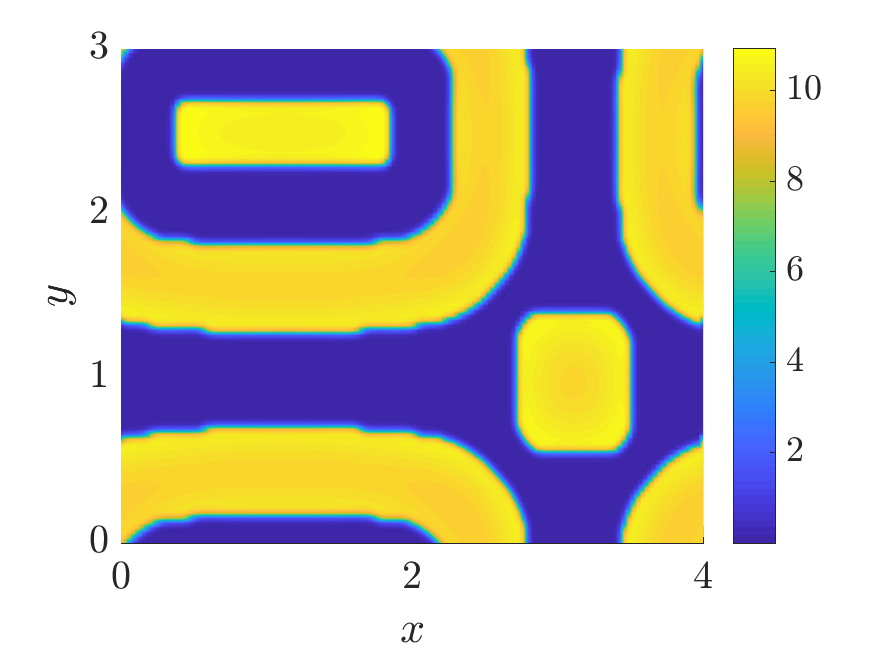
In this paper we analyse a finite volume scheme for a nonlocal version of the Shigesada-Kawazaki-Teramoto (SKT) cross-diffusion system. We prove the existence of solutions to the scheme, derive qualitative properties of the solutions and prove its convergence. The proofs rely on a discrete entropy-dissipation inequality, discrete compactness arguments, and on the novel adaptation of the so-called duality method at the discrete level. Finally, thanks to numerical experiments, we investigate the influence of the nonlocality in the system: on convergence properties of the scheme, as an approximation of the local system and on the development of diffusive instabilities.