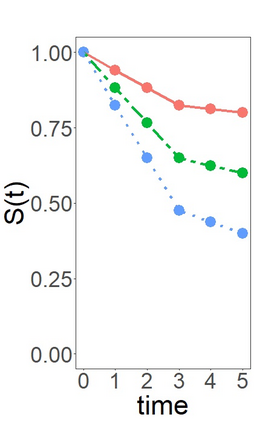
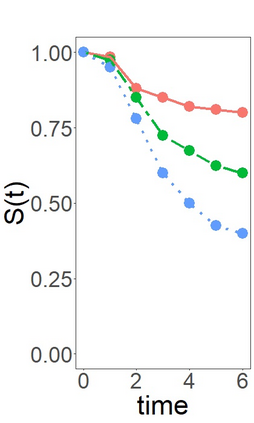
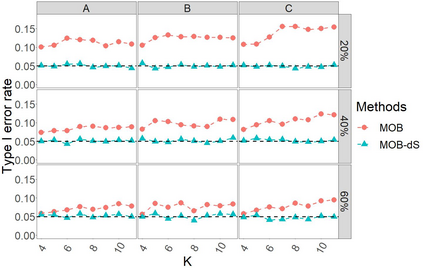
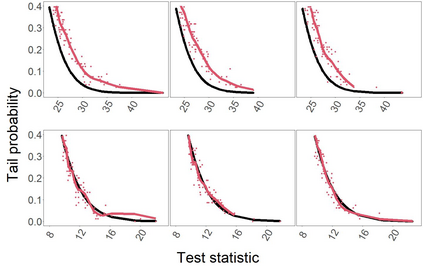
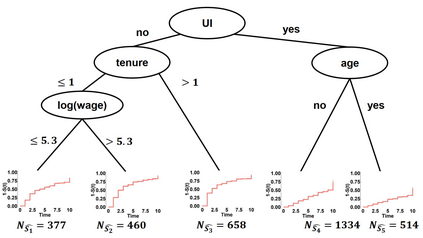
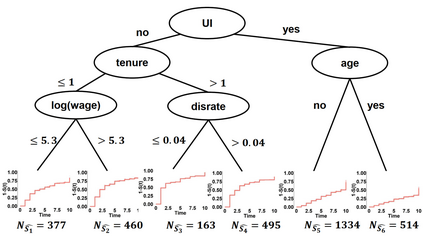
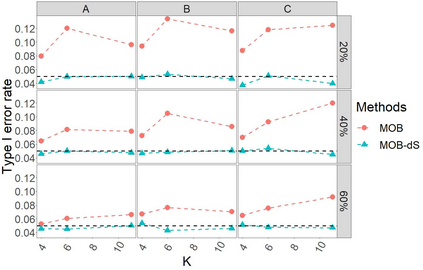
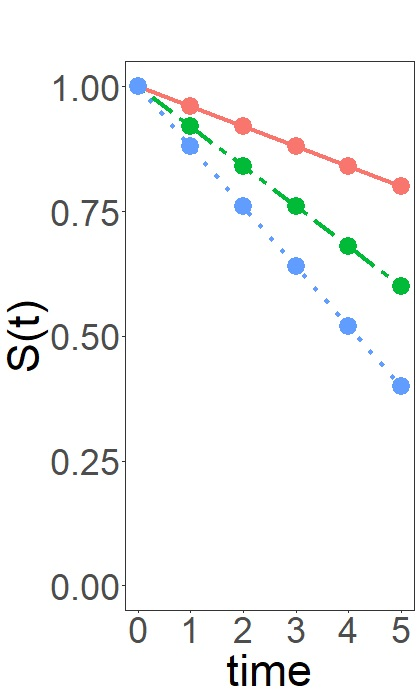
Model-based recursive partitioning (MOB) is a semi-parametric statistical approach allowing the identification of subgroups that can be combined with a broad range of outcome measures including continuous time-to-event outcomes. When time is measured on a discrete scale, methods and models need to account for this discreetness as otherwise subgroups might be spurious and effects biased. The test underlying the splitting criterion of MOB, the M-fluctuation test, assumes independent observations. However, for fitting discrete time-to-event models the data matrix has to be modified resulting in an augmented data matrix violating the independence assumption. We propose MOB for discrete Survival data (MOB-dS) which controls the type I error rate of the test used for data splitting and therefore the rate of identifying subgroups although none is present. MOB-ds uses a permutation approach accounting for dependencies in the augmented time-to-event data to obtain the distribution under the null hypothesis of no subgroups being present. Through simulations we investigate the type I error rate of the new MOB-dS and the standard MOB for different patterns of survival curves and event rates. We find that the type I error rates of the test is well controlled for MOB-dS, but observe some considerable inflations of the error rate for MOB. To illustrate the proposed methods, MOB-dS is applied to data on unemployment duration.
翻译:以模型为基础的递归分割法(MOB)是一种半参数统计方法,它允许确定可与一系列广泛结果措施相结合的分组,包括连续的时间到活动结果。当在一个离散的尺度上测量时间时,方法和模型需要说明这种谨慎性,因为其他分组可能是假的,效果也存在偏差。MOB的分解标准所依据的测试是独立的观测,但对于适当的离散时间到活动模型而言,数据矩阵必须加以修改,从而导致违反独立假设的扩大数据矩阵。我们建议,对于独立的生存数据(MOB-dS)提出MOB,用于控制数据分解所用测试的I型错误率,因此,方法和模型需要将这种谨慎性考虑在内,因为其他分组可能是假的,结果有偏差。MOB-d使用一种调整方法来计算在扩大的时间到事件表中的相互依赖性,以获得在任何分组的无效假设下分配数据。我们通过模拟来调查新的MOB-dS应用的I型错误率,而MOB标准值为不同生存率模式的MOB的精确率。