Information-Theoretic Registration with Explicit Reorientation of Diffusion-Weighted Images

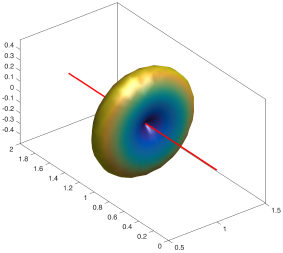
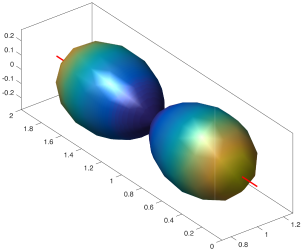
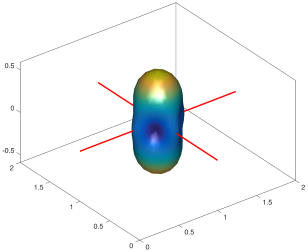
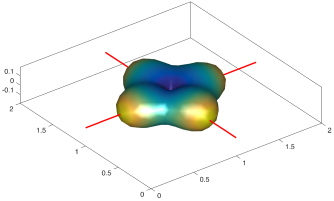
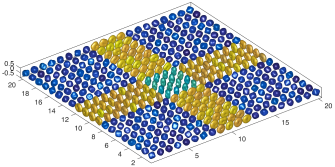
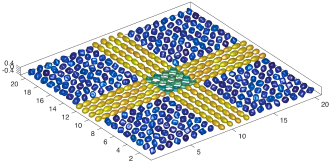
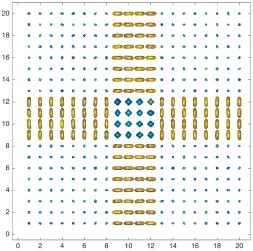
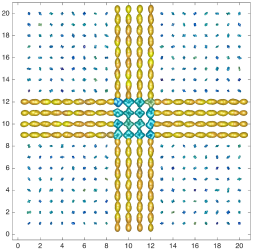
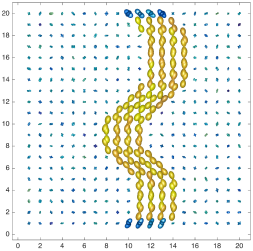
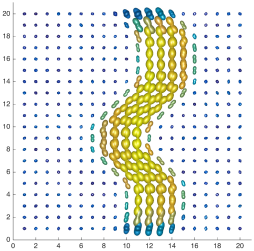
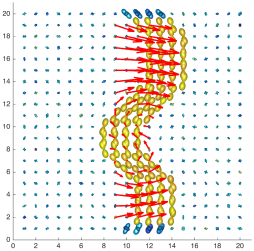
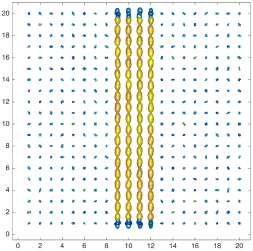
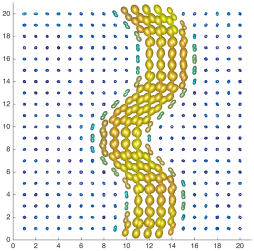
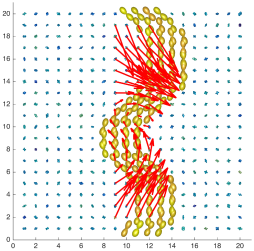
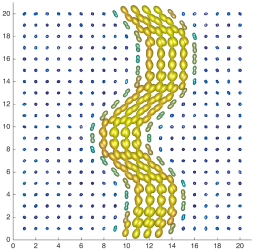
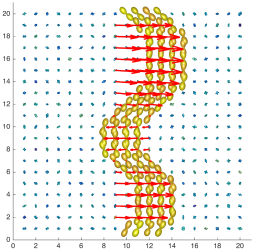
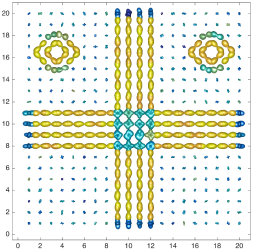
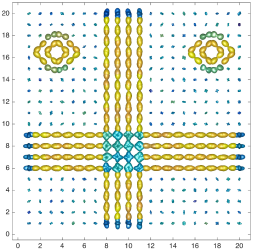
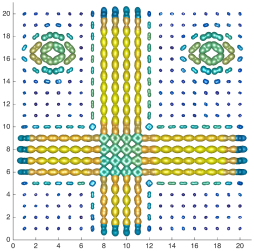
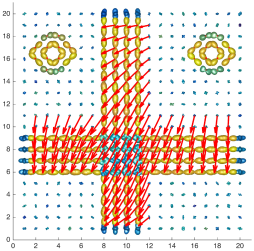
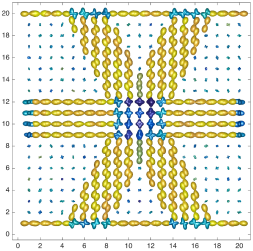
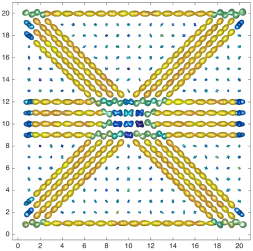
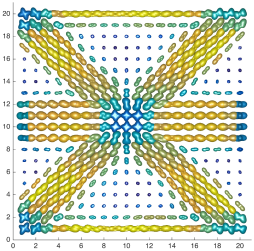
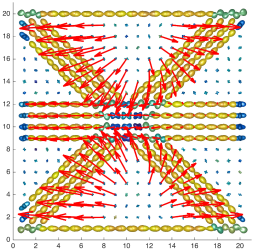
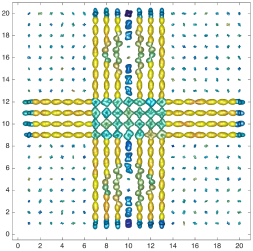
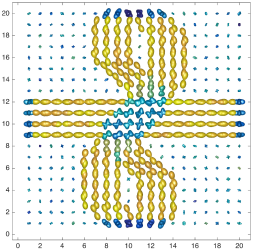
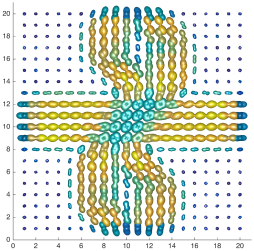
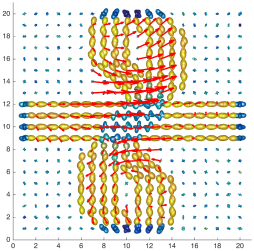
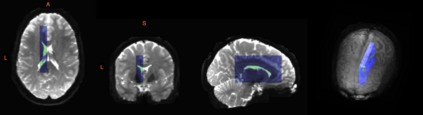
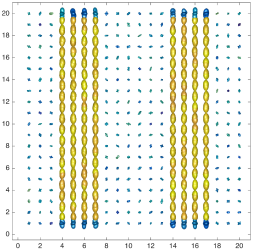
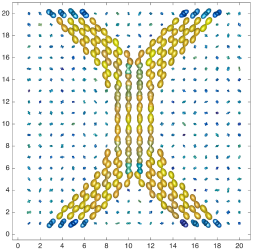
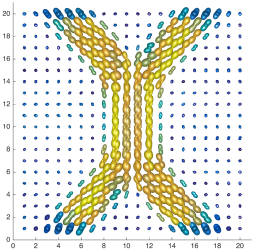
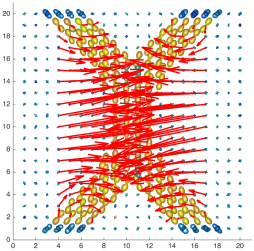
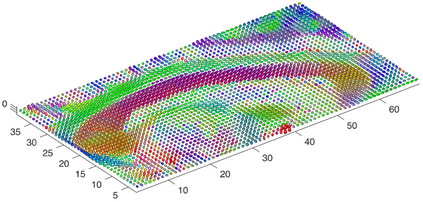
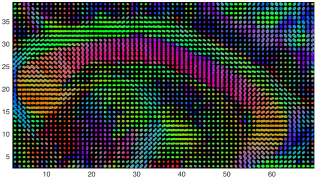
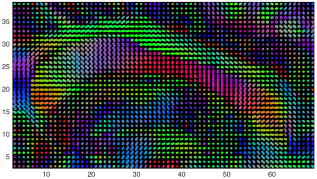
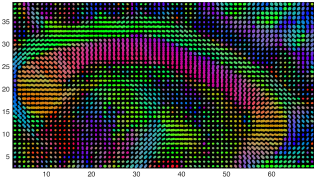
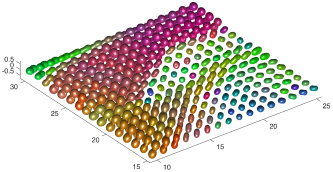
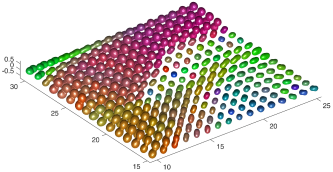
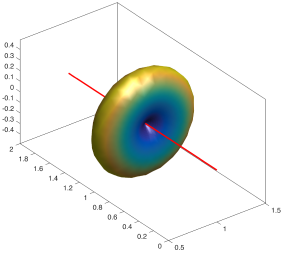
We present an information-theoretic approach to the registration of images with directional information, and especially for diffusion-Weighted Images (DWI), with explicit optimization over the directional scale. We call it Locally Orderless Registration with Directions (LORD). We focus on normalized mutual information as a robust information-theoretic similarity measure for DWI. The framework is an extension of the LOR-DWI density-based hierarchical scale-space model that varies and optimizes the integration, spatial, directional, and intensity scales. As affine transformations are insufficient for inter-subject registration, we extend the model to non-rigid deformations. We illustrate that the proposed model deforms orientation distribution functions (ODFs) correctly and is capable of handling the classic complex challenges in DWI-registrations, such as the registration of fiber-crossings along with kissing, fanning, and interleaving fibers. Our experimental results clearly illustrate a novel promising regularizing effect, that comes from the nonlinear orientation-based cost function. We show the properties of the different image scales and, we show that including orientational information in our model makes the model better at retrieving deformations in contrast to standard scalar-based registration.