On the stability of conservative discontinuous Galerkin/Hermite spectral methods for the Vlasov-Poisson system

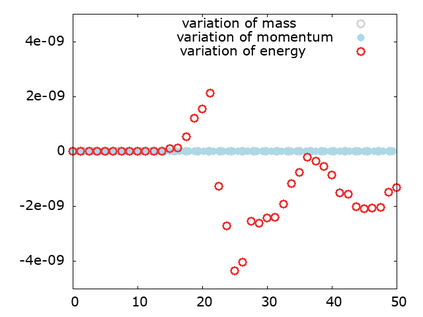
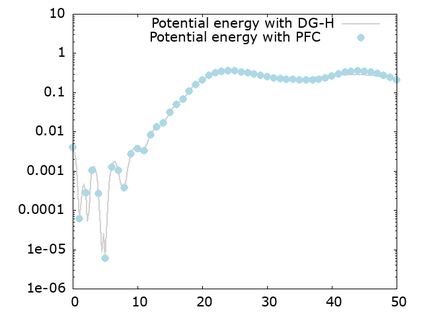
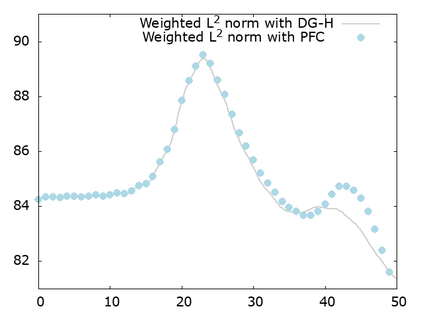
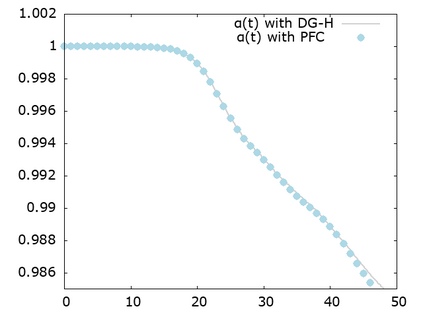
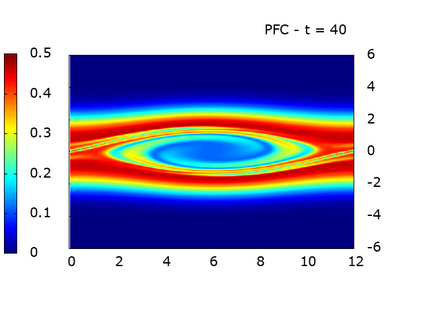
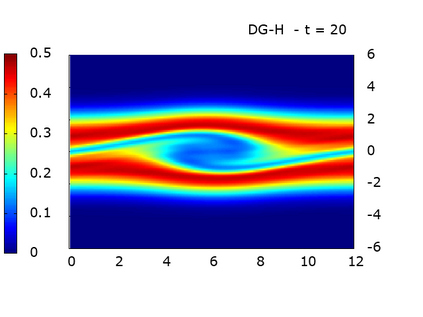
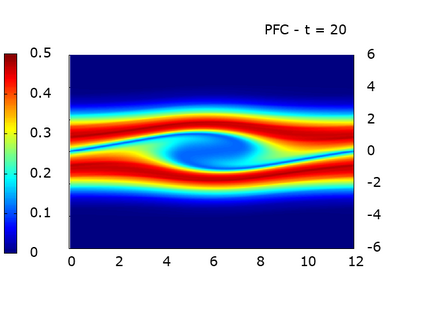
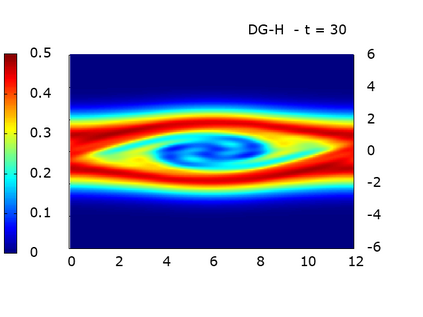
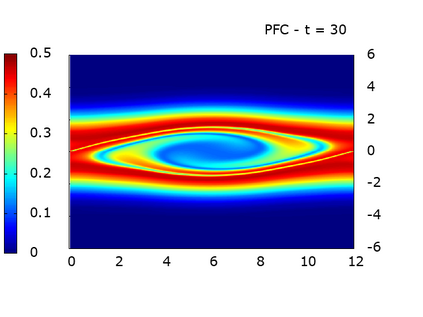
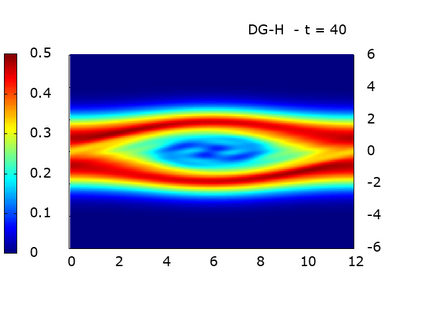
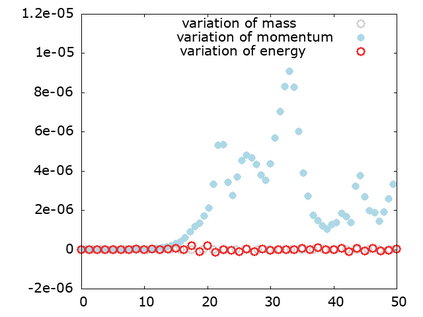
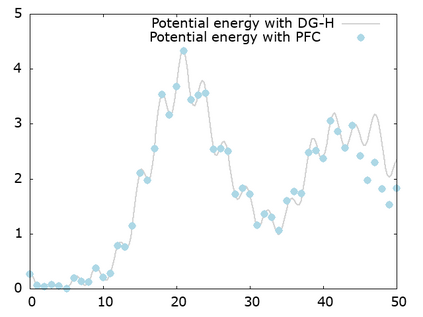
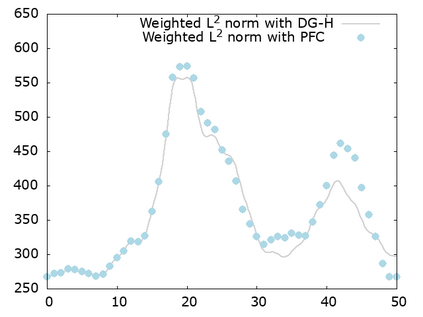
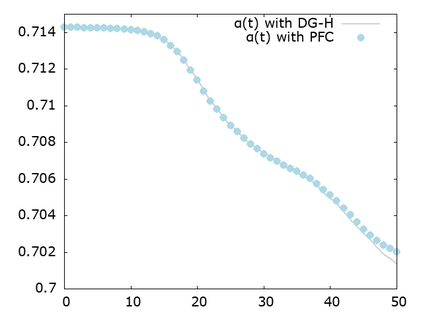
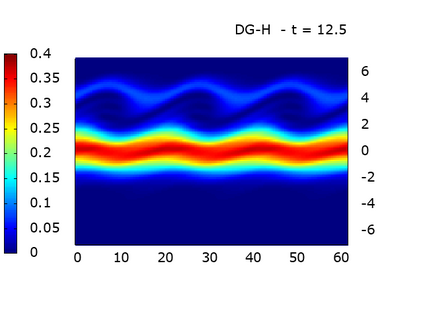
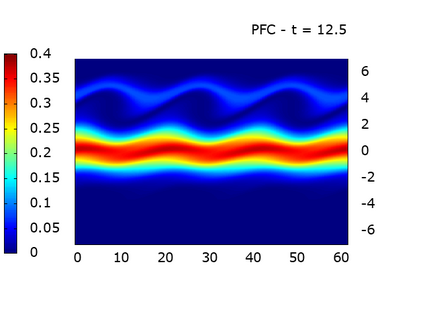
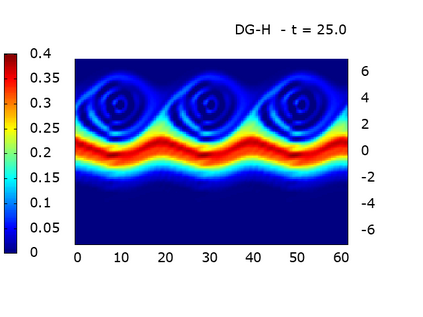
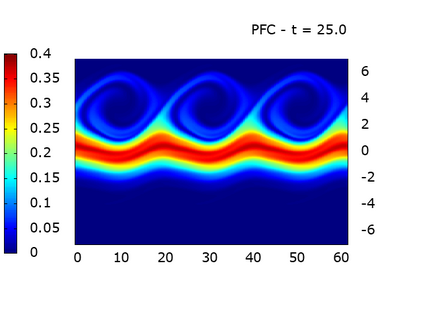
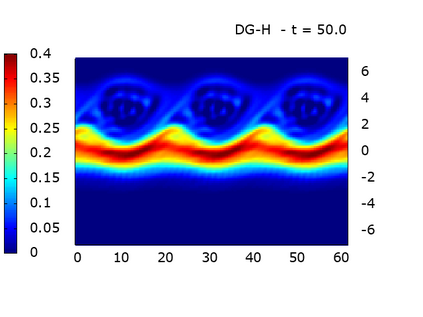
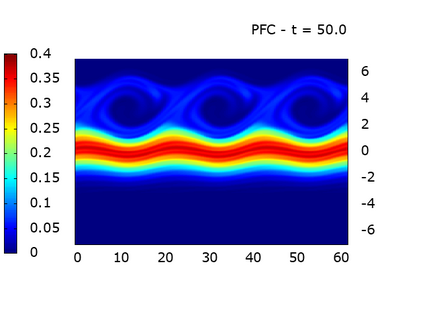
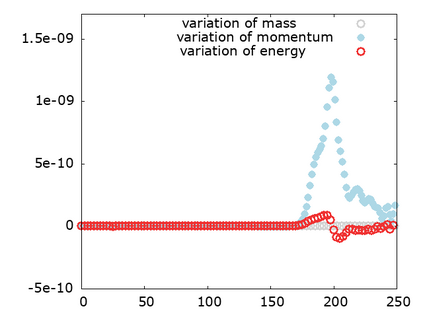
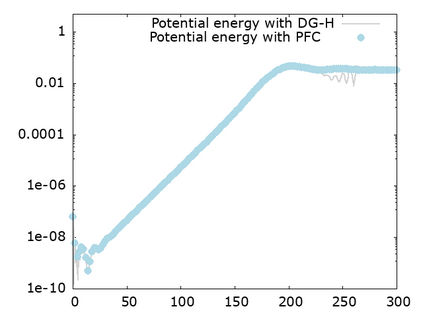
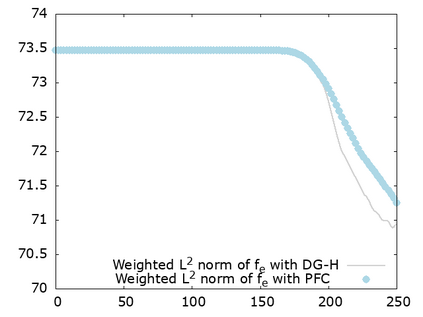
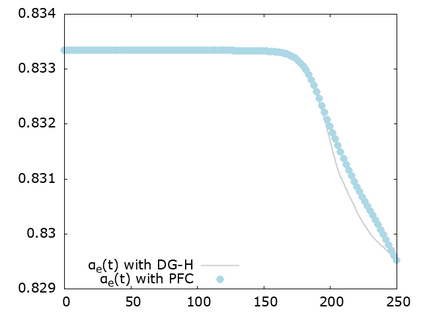
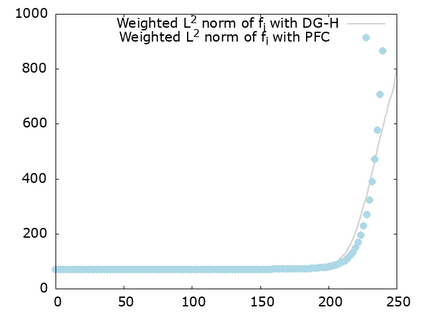
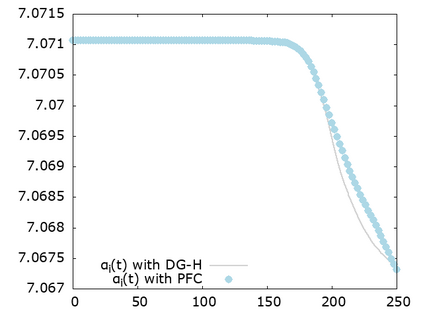
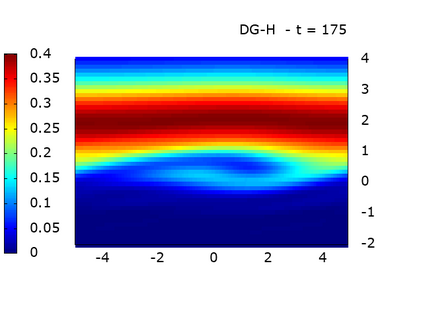
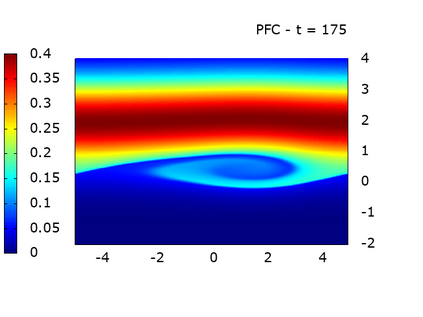
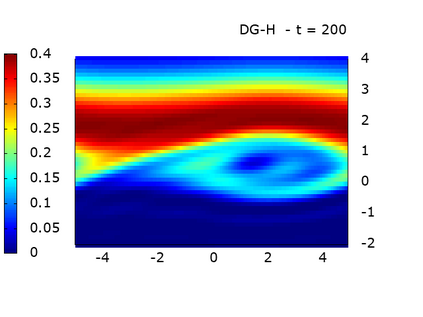
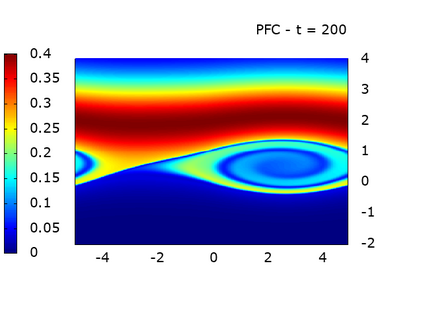
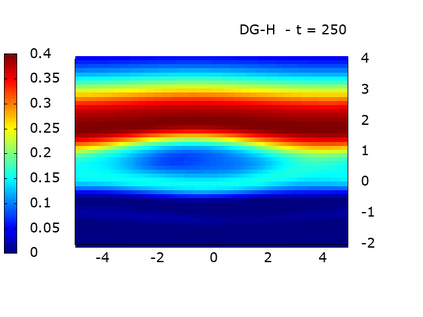
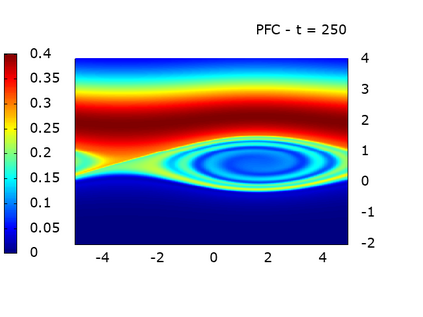
We study a class of spatial discretizations for the Vlasov-Poisson system written as an hyperbolic system using Hermite polynomials. In particular, we focus on spectral methods and discontinuous Galerkin approximations. To obtain L 2 stability properties, we introduce a new L 2 weighted space, with a time dependent weight. For the Hermite spectral form of the Vlasov-Poisson system, we prove conservation of mass, momentum and total energy, as well as global stability for the weighted L 2 norm. These properties are then discussed for several spatial discretizations. Finally, numerical simulations are performed with the proposed DG/Hermite spectral method to highlight its stability and conservation features.