强化学习最优表示的几何视角（A Geometric Perspective on Optimal Representations for Reinforcement Learning）

题目： A Geometric Perspective on Optimal Representations for Reinforcement Learning

摘要：

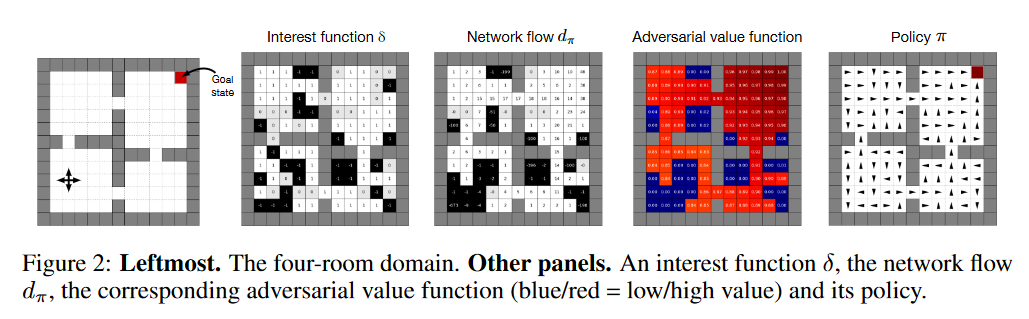
在这篇论文中提出了一种基于值函数空间几何性质的表示学习方法。我们利用这个观点来提供关于价值函数作为辅助任务的有用性的正式证据。我们的公式考虑调整表示法来最小化给定环境中所有平稳策略的值函数的(线性)近似。我们证明了这种优化简化为对一类特殊的值函数(我们称之为对抗性值函数(AVFs))进行准确的预测。我们证明了使用值函数作为辅助任务对应于我们的公式的期望误差松弛，AVFs是一个自然的候选，并确定了与原值函数的密切关系。我们在一系列域实验中强调了AVFs的特点及其作为辅助任务的实用性。

作者：

Marc G. Bellemare是加拿大蒙特利尔谷歌大脑的一名研究科学家，专注于强化学习，之前在阿尔伯塔大学获得了博士学位，研究领域是强化学习和概率预测的交叉领域，还对深度学习、生成模型、在线学习和信息论感兴趣。个人官网：http://www.marcgbellemare.info/

Nicolas Le Roux是现在是蒙特利尔谷歌大脑优化项目的负责人，也是麦吉尔大学的兼职教授。研究领域是机器学习，神经网络，优化，大规模学习和统计建模。个人官网：http://nicolas.le-roux.name/