On the recursive structure of multigrid cycles

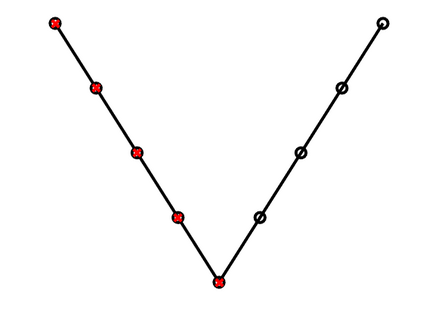
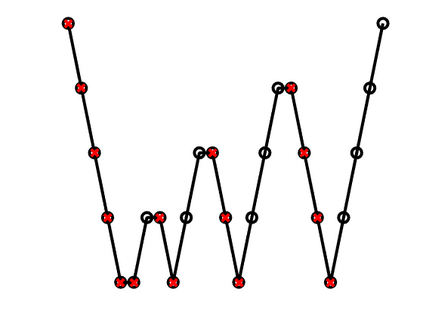
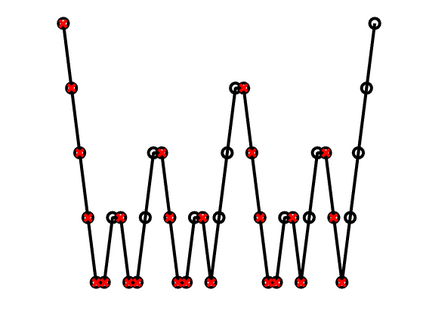
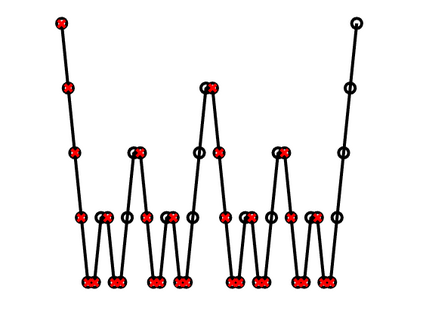
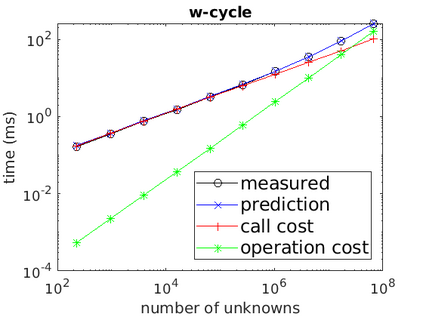
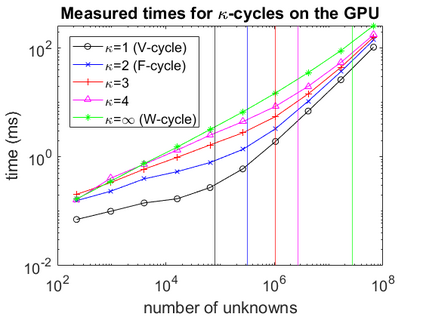
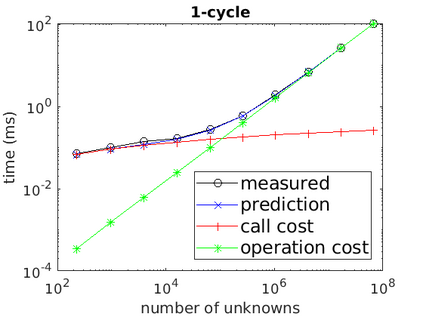
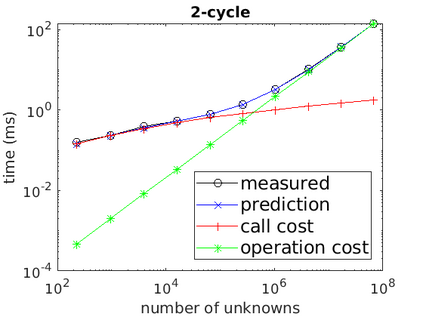
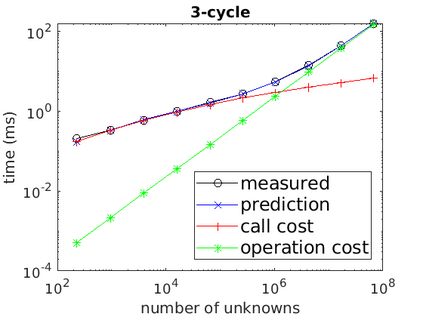
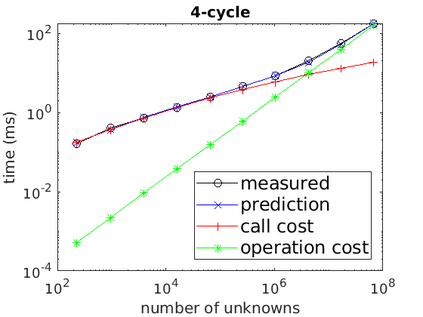
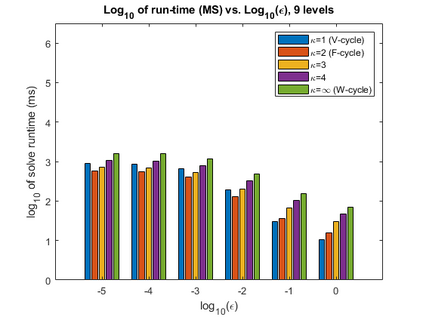
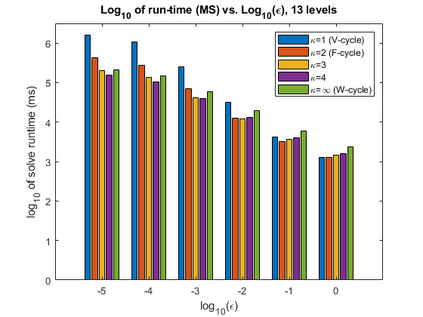
A new fixed (non-adaptive) recursive scheme for multigrid algorithms is introduced. Governed by a positive parameter $\kappa$ called the cycle counter, this scheme generates a family of multigrid cycles dubbed $\kappa$-cycles. The well-known $V$-cycle, $F$-cycle, and $W$-cycle are shown to be particular members of this rich $\kappa$-cycle family, which satisfies the property that the total number of recursive calls in a single cycle is a polynomial of degree $\kappa$ in the number of levels of the cycle. This broadening of the scope of fixed multigrid cycles is shown to be potentially significant for the solution of some large problems on platforms, such as GPU processors, where the overhead induced by recursive calls may be relatively significant. In cases of problems for which the convergence of standard $V$-cycles or $F$-cycles (corresponding to $\kappa=1$ and $\kappa=2$, respectively) is particularly slow, and yet the cost of $W$-cycles is very high due to the large number of recursive calls (which is exponential in the number of levels), intermediate values of $\kappa$ may prove to yield significantly faster run-times. This is demonstrated in examples where $\kappa$-cycles are used for the solution of rotated anisotropic diffusion problems, both as a stand-alone solver and as a preconditioner. Moreover, a simple model is presented for predicting the approximate run-time of the $\kappa$-cycle, which is useful in pre-selecting an appropriate cycle counter for a given problem on a given platform. Implementing the $\kappa$-cycle requires making just a small change in the classical multigrid cycle.