Query-Based Selection of Optimal Candidates under the Mallows Model

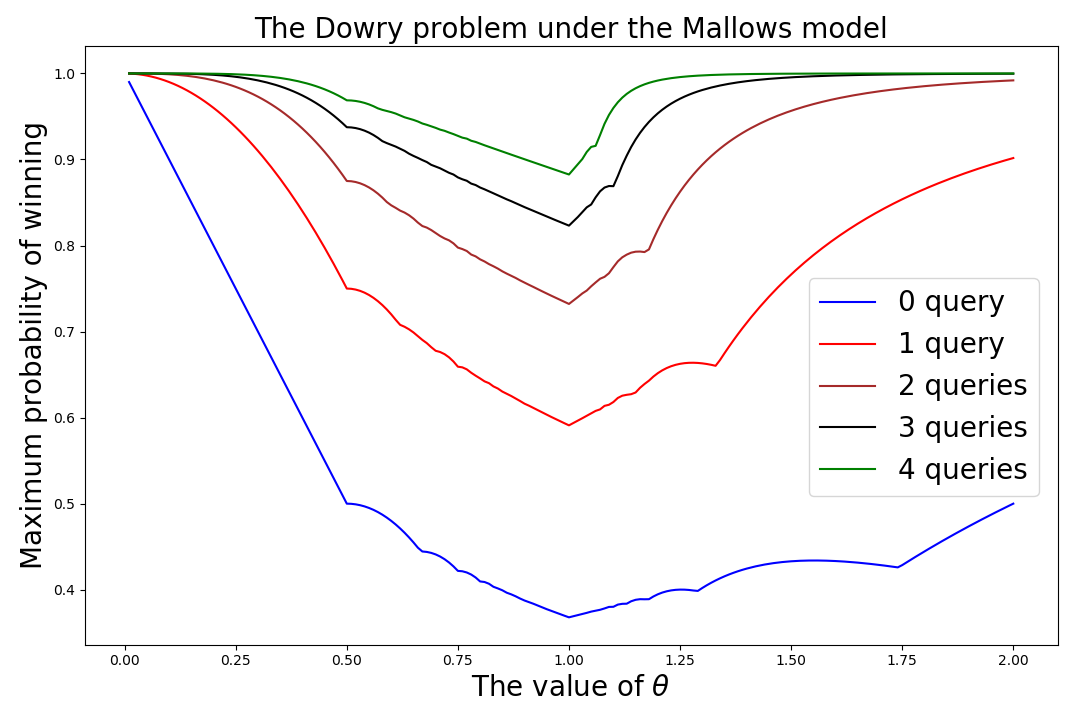
We introduce the problem of query-based selection of the optimal candidate in rank-ordered lists generated by the Mallows model. In this setting, one is presented with a list of candidates drawn according to a Gaussian-like distribution for permutations and the goal is to identify the highest ranked candidate through a sequential interview process that does not allow rejected candidates to be revisited. The new modeling assumption consists in being able to query a Genie at the time a selection is to be made. The query provides an answer indicating if the candidate in question is the highest-ranked or not. If the Genie confirms the query, the selection process terminates. Otherwise, the sequential examinations continue until a new potentially optimal candidate is identified. Our results include optimal interview strategies for a bounded number of queries that can be exactly determined through numerical evaluations as well as the expected number of interviews until the optimal candidate is identified or the interview process completed. Although the problem exhibits similarities with the Dowry problem with multiple choices of Gilbert and Mosteller, the proposed Genie-based model substantially differs from it as it allows for early stopping and addresses nonuniform candidate interview distributions.