Bivariate vine copula based quantile regression

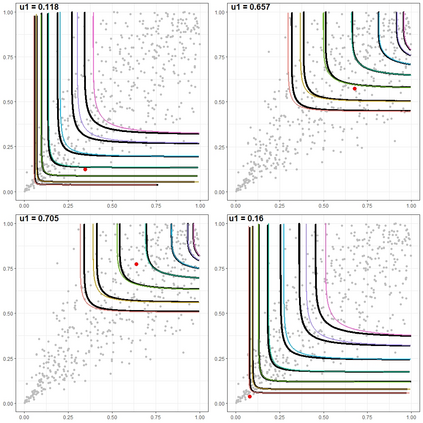
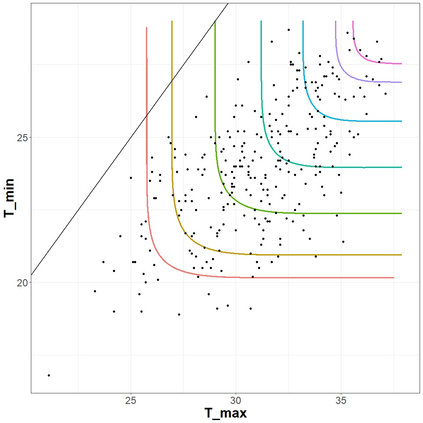
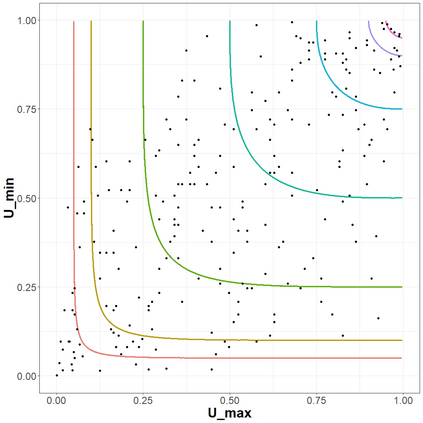
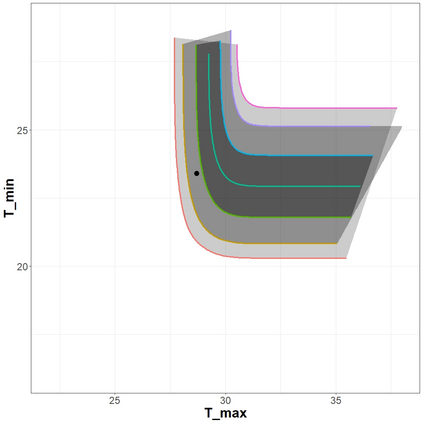
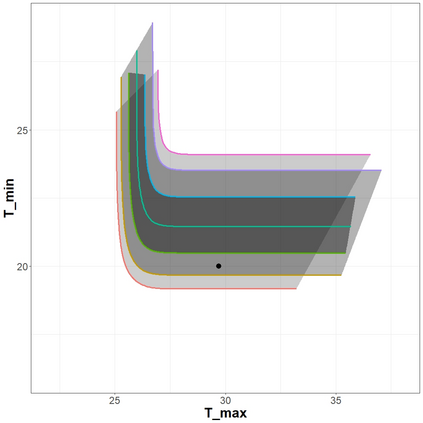
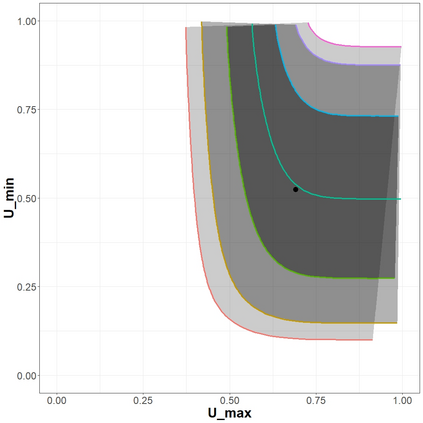
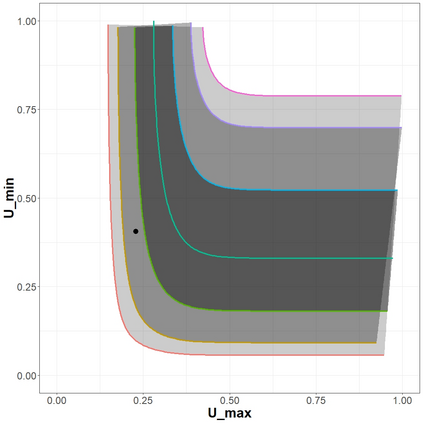
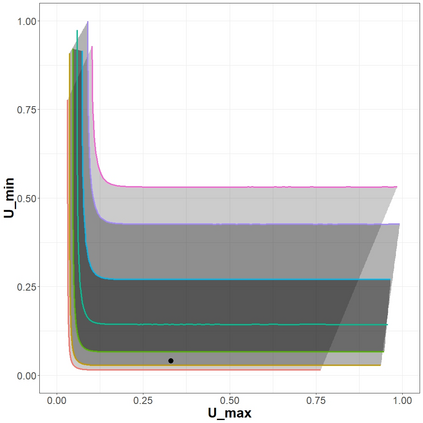
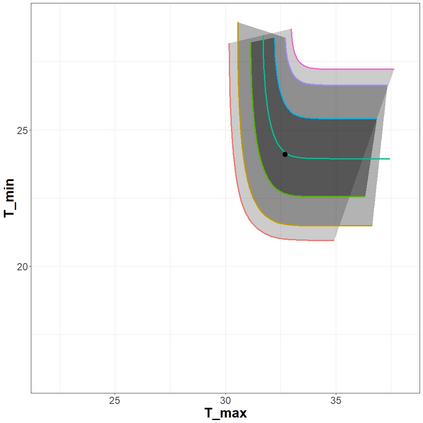
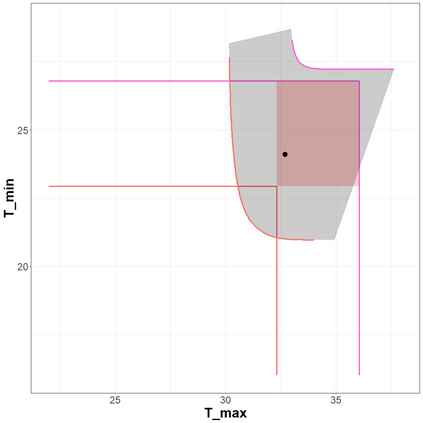
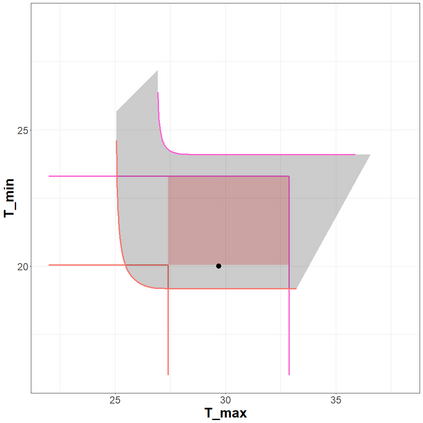
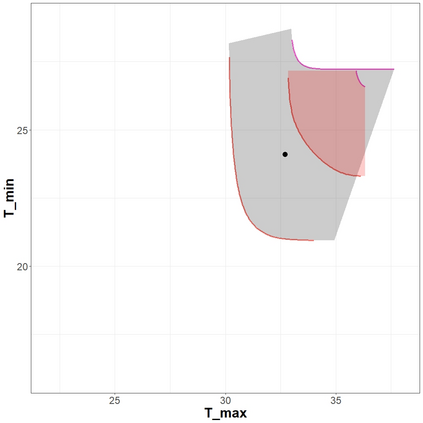
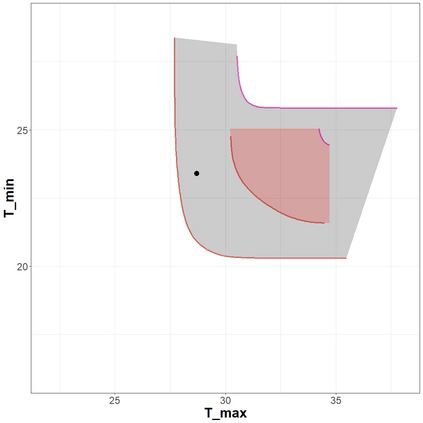
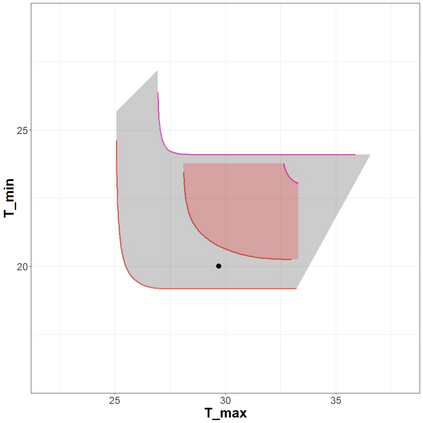
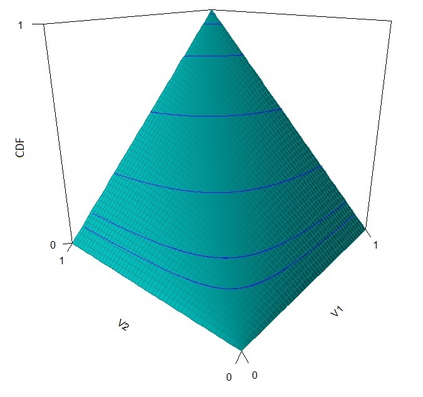
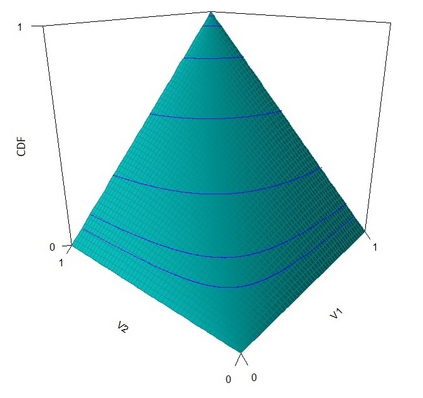
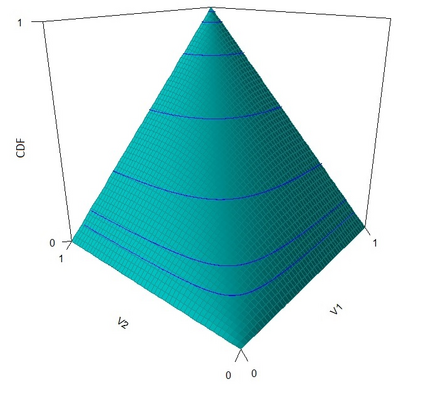
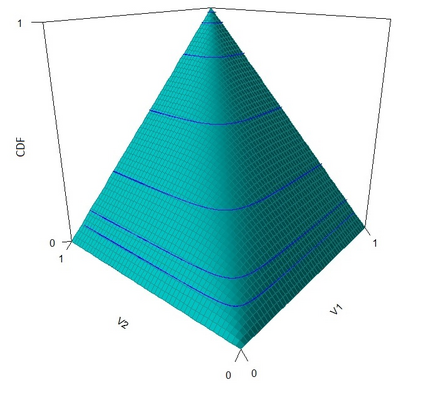
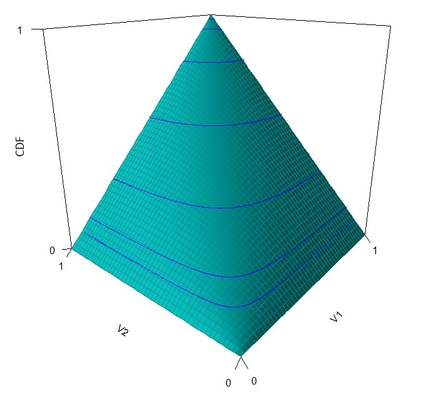
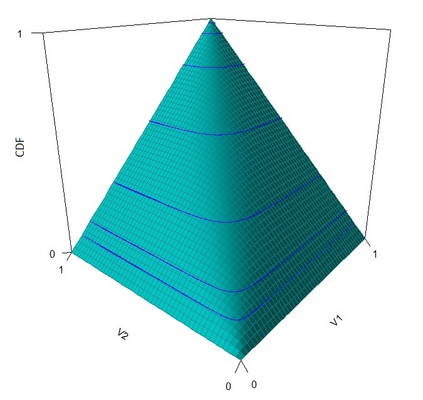
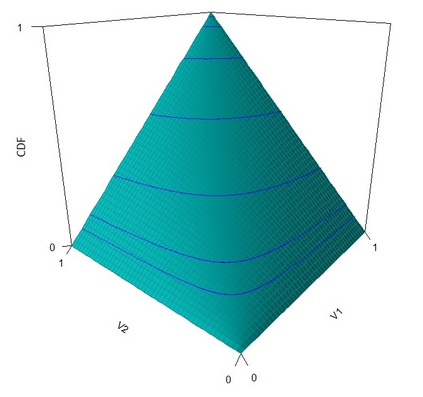
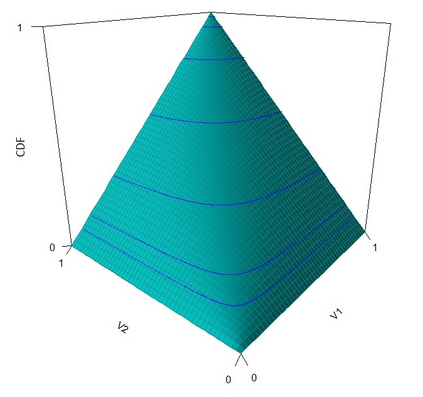
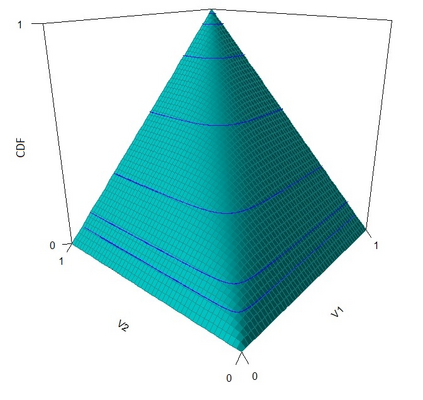
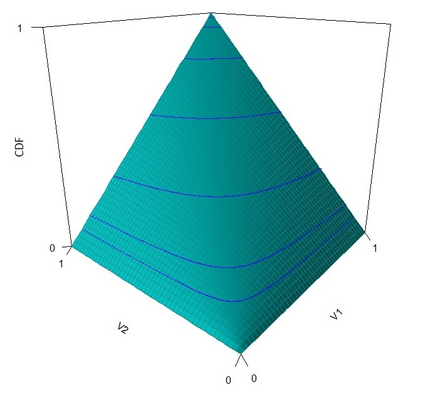
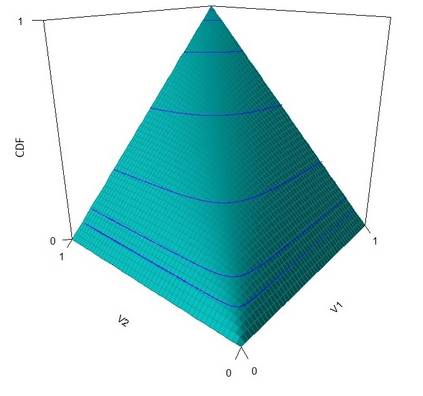
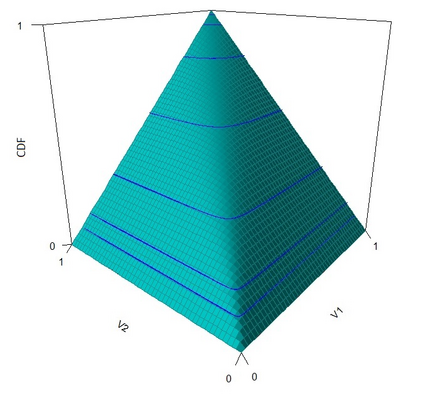
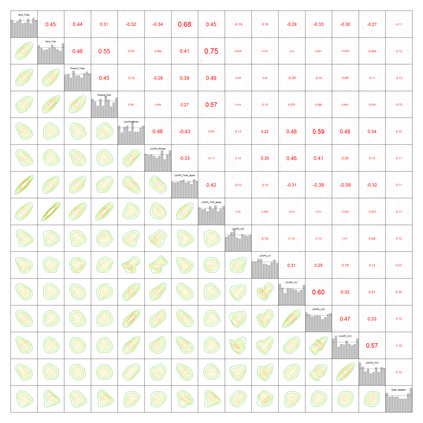
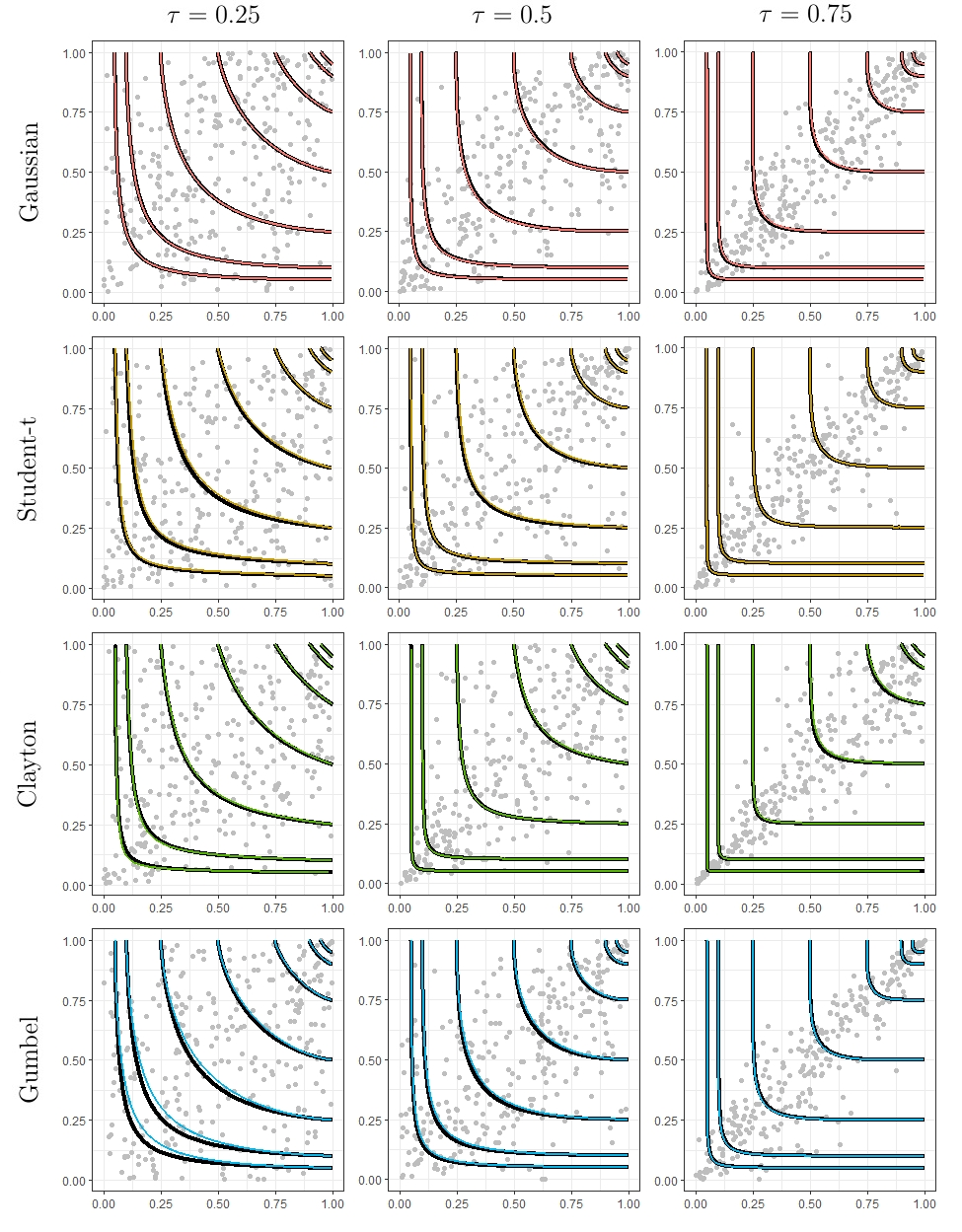
The statistical analysis of univariate quantiles is a well developed research topic. However, there is a profound need for research in multivariate quantiles. We tackle the topic of bivariate quantiles and bivariate quantile regression using vine copulas. They are graph theoretical models identified by a sequence of linked trees, which allow for separate modelling of marginal distributions and the dependence structure. We introduce a novel graph structure model (given by a tree sequence) specifically designed for a symmetric treatment of two responses in a predictive regression setting. We establish computational tractability of the model and a straight forward way of obtaining different conditional distributions. Using vine copulas the typical shortfalls of regression, as the need for transformations or interactions of predictors, collinearity or quantile crossings are avoided. We illustrate the copula based bivariate quantiles for different copula distributions and provide a data set example. Further, the data example emphasizes the benefits of the joint bivariate response modelling in contrast to two separate univariate regressions or by assuming conditional independence, for bivariate response data set in the presence of conditional dependence.