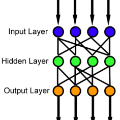
This paper explores the topological signatures of ReLU neural network activation patterns. We consider feedforward neural networks with ReLU activation functions and analyze the polytope decomposition of the feature space induced by the network. Mainly, we investigate how the Fiedler partition of the dual graph and show that it appears to correlate with the decision boundary -- in the case of binary classification. Additionally, we compute the homology of the cellular decomposition -- in a regression task -- to draw similar patterns in behavior between the training loss and polyhedral cell-count, as the model is trained.
翻译:暂无翻译
相关内容
Networking:IFIP International Conferences on Networking。
Explanation:国际网络会议。
Publisher:IFIP。
SIT: http://dblp.uni-trier.de/db/conf/networking/index.html
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日