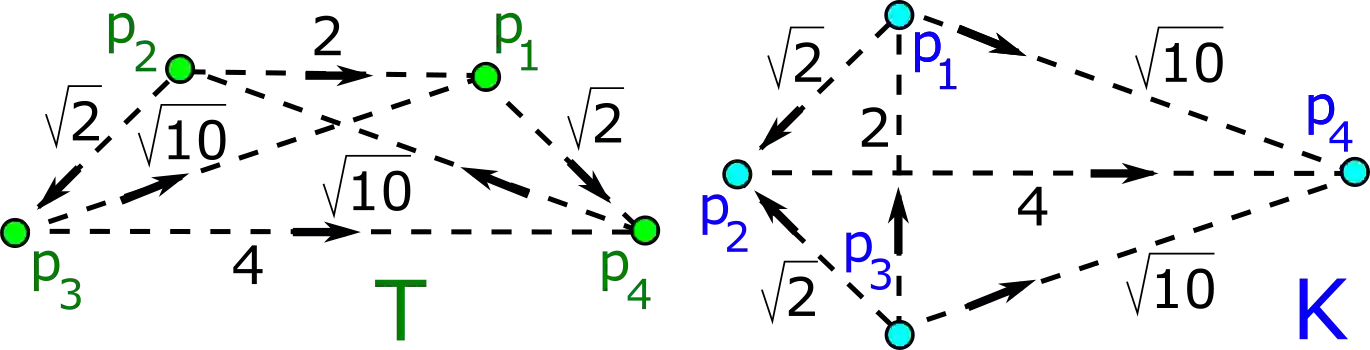
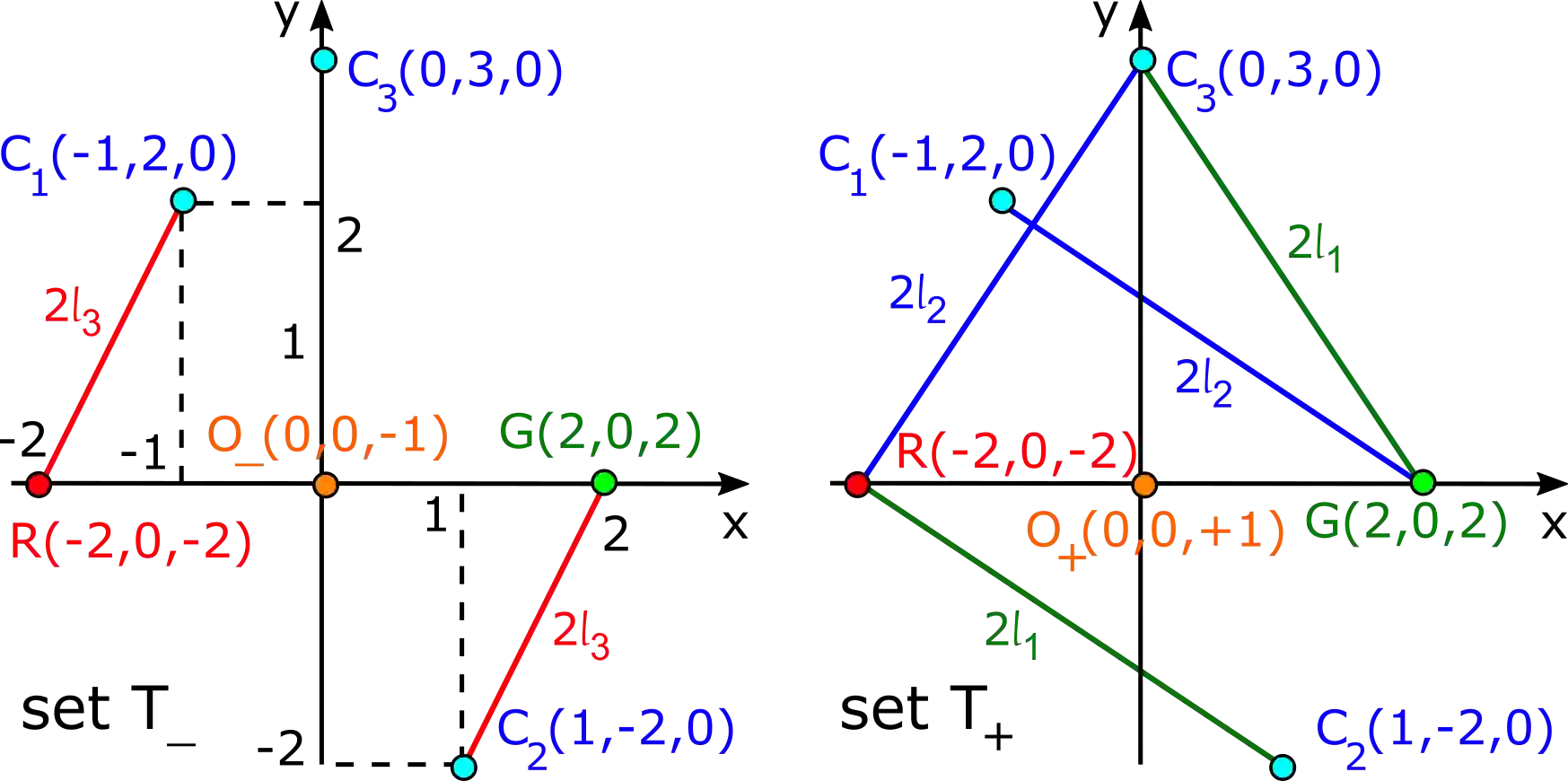
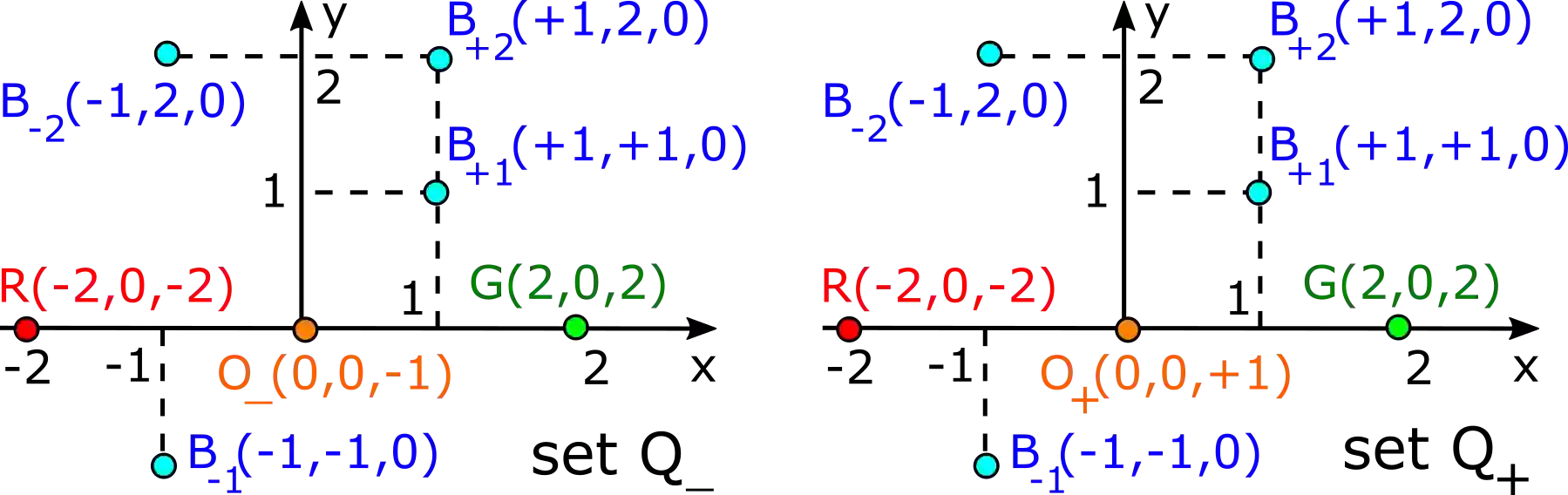A finite set of unlabelled points in Euclidean space is the simplest representation of many real objects from mineral rocks to sculptures. Since most solid objects are rigid, their natural equivalence is rigid motion or isometry maintaining all inter-point distances. More generally, any finite metric space is an example of a metric-measure space that has a probability measure and a metric satisfying all axioms. This paper develops Simplexwise Distance Distributions (SDDs) for any finite metric spaces and metric-measures spaces. These SDDs classify all known non-equivalent spaces that were impossible to distinguish by simpler invariants. We define metrics on SDDs that are Lipschitz continuous and allow exact computations whose parametrised complexities are polynomial in the number of given points.
翻译:在欧几里得空间中,一组未标记的有限点是许多实际对象的最简表示,从矿物岩石到雕塑。由于大多数固体物体都是刚体,它们的自然等价性是保持所有点距离不变的等距变换或同构。更一般地,任何有限测度空间都是一个具有概率测度和度量,满足所有公理的度量-测度空间的例子。本文针对任意有限测度空间和度量-测度空间,提出了简单形式下的距离分布(SDD)的概念。这些SDD对于许多不同的已知互不等价的空间进行分类,而这些空间无法通过更简单的不变量进行区分。我们定义了SDD上的度量,这些度量是Lipschitz连续的,并允许精确计算,其参数化复杂性多项式地依赖于给定点的数量。