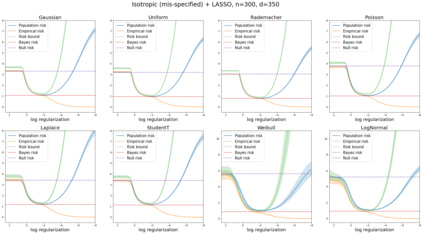
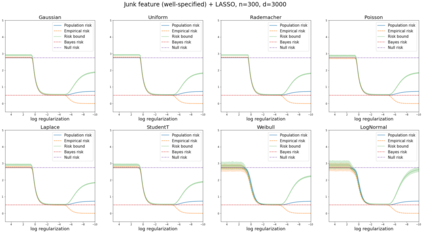
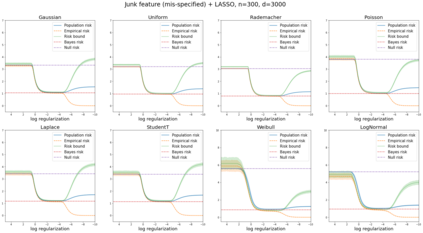
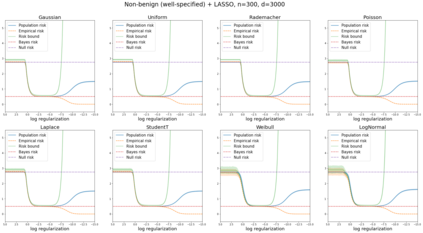
We prove a new generalization bound that shows for any class of linear predictors in Gaussian space, the Rademacher complexity of the class and the training error under any continuous loss $\ell$ can control the test error under all Moreau envelopes of the loss $\ell$. We use our finite-sample bound to directly recover the "optimistic rate" of Zhou et al. (2021) for linear regression with the square loss, which is known to be tight for minimal $\ell_2$-norm interpolation, but we also handle more general settings where the label is generated by a potentially misspecified multi-index model. The same argument can analyze noisy interpolation of max-margin classifiers through the squared hinge loss, and establishes consistency results in spiked-covariance settings. More generally, when the loss is only assumed to be Lipschitz, our bound effectively improves Talagrand's well-known contraction lemma by a factor of two, and we prove uniform convergence of interpolators (Koehler et al. 2021) for all smooth, non-negative losses. Finally, we show that application of our generalization bound using localized Gaussian width will generally be sharp for empirical risk minimizers, establishing a non-asymptotic Moreau envelope theory for generalization that applies outside of proportional scaling regimes, handles model misspecification, and complements existing asymptotic Moreau envelope theories for M-estimation.
翻译:我们用有限的样本直接恢复周等人(2021年)的“乐观率”与平方损失的“乐观率”(2021年)的线性回归,据了解,平方损失对于最低程度的精确度调值而言是十分紧凑的,但是我们也处理更一般的设置,在这种设置中,标签是由可能错误指定的多指数模型生成的。同样的论点可以分析最大间差分类器通过方形断层损失产生的杂音间推,并在高方形变异环境中确定一致性结果。更一般地说,当损失仅被假定为利普施奇茨时,我们就会有效地改进塔拉格兰(Talagrand)众所周知的精度缩缩缩缩模型,以2倍的平整度来补充,而我们则证明,对于所有平滑的、非正向型断层分类模型来说,内化(Koehler et al. 2021年)是统一的。最后,我们用更清晰的超度理论来证明,对于整个平滑、非正匀的深度的超度理论来说,我们用一个非高度的缩缩的模型来证明我们一般的缩缩缩缩缩缩的风险。