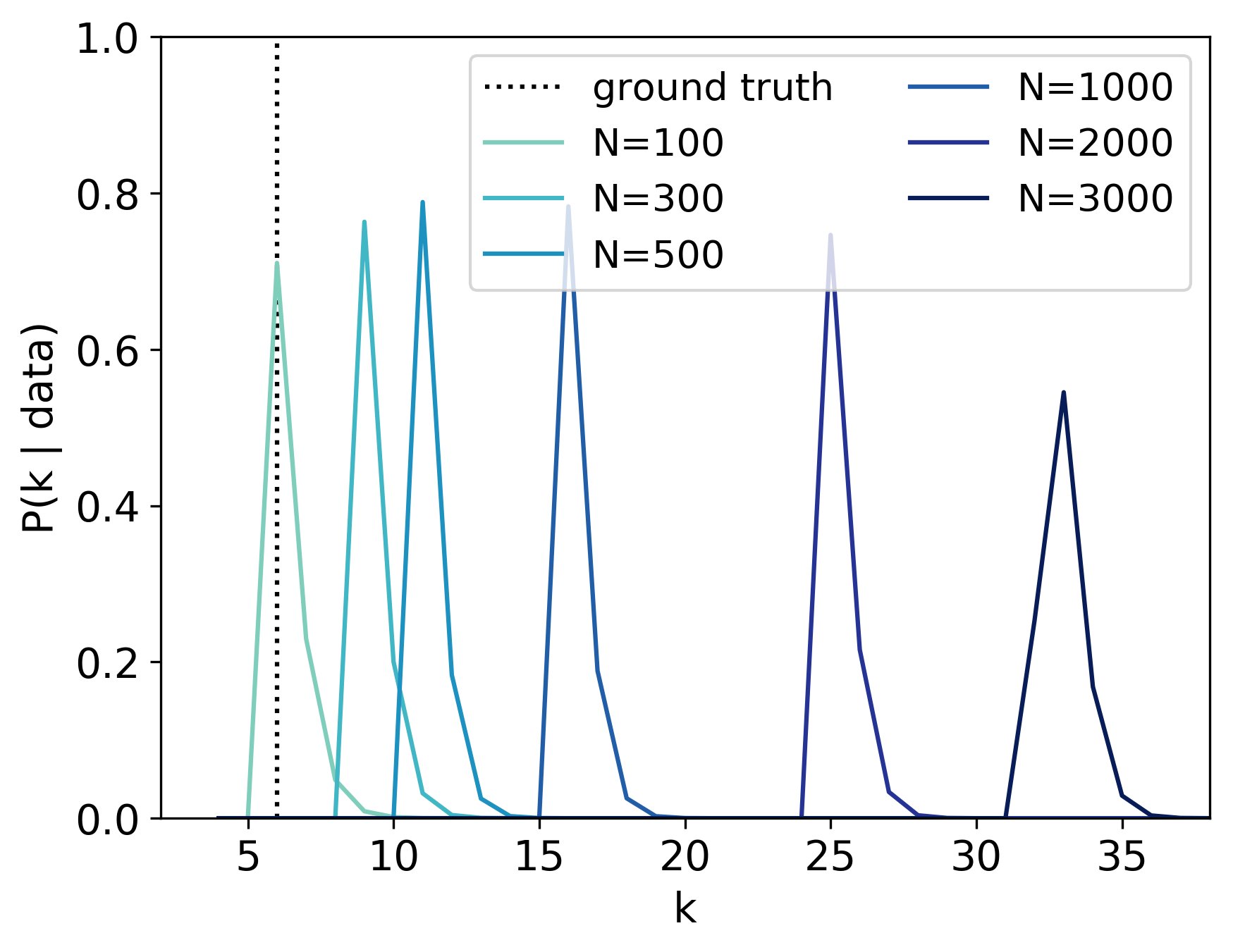
Scientists and engineers are often interested in learning the number of subpopulations (or components) present in a data set. A common suggestion is to use a finite mixture model (FMM) with a prior on the number of components. Past work has shown the resulting FMM component-count posterior is consistent; that is, the posterior concentrates on the true, generating number of components. But consistency requires the assumption that the component likelihoods are perfectly specified, which is unrealistic in practice. In this paper, we add rigor to data-analysis folk wisdom by proving that under even the slightest model misspecification, the FMM component-count posterior diverges: the posterior probability of any particular finite number of components converges to 0 in the limit of infinite data. Contrary to intuition, posterior-density consistency is not sufficient to establish this result. We develop novel sufficient conditions that are more realistic and easily checkable than those common in the asymptotics literature. We illustrate practical consequences of our theory on simulated and real data.
翻译:科学家和工程师往往有兴趣了解数据集中存在的亚群数(或组成部分)的数量。一个共同的建议是使用一个具有先验成分数量的有限混合模型(FMM),先验的成分数量。过去的工作表明,由此得出的FMM的成分计数后背体是一致的;也就是说,后成体集中在真实的成分上,产生大量成分。但一致性要求假设组成部分的可能性是完全具体的,在实践中是不切实际的。在本文中,我们通过证明在即使是最微小的模型中,FMM的成分计数后表层差异:在无限数据限度内,任何特定有限成分数的后验概率会达到0。与直觉相反,后成体密度的连贯性并不足以确立这一结果。我们开发出比非典型文献中常见的更现实和容易核对的新的充分条件。我们举例说明了我们关于模拟和真实数据理论的实际后果。