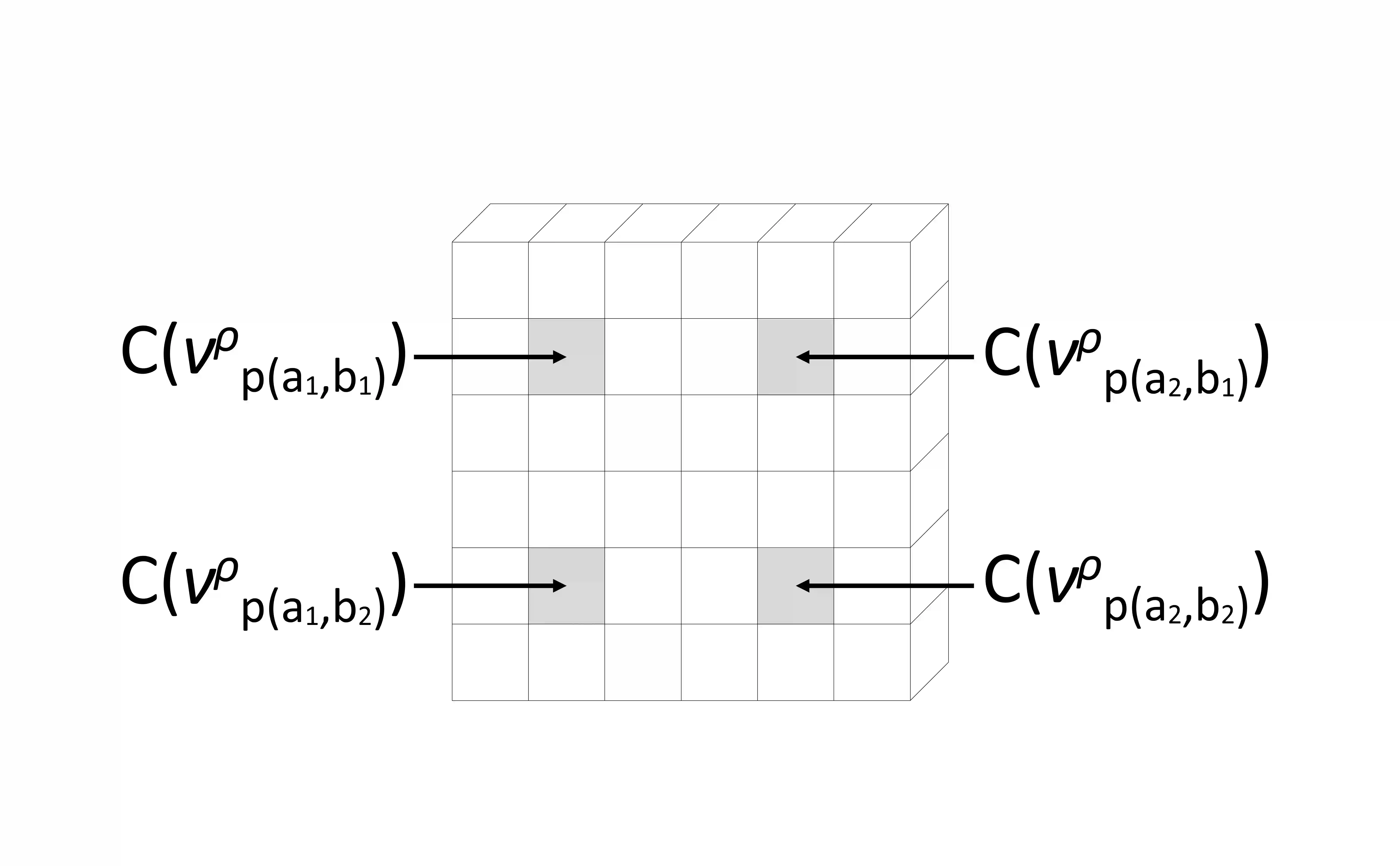
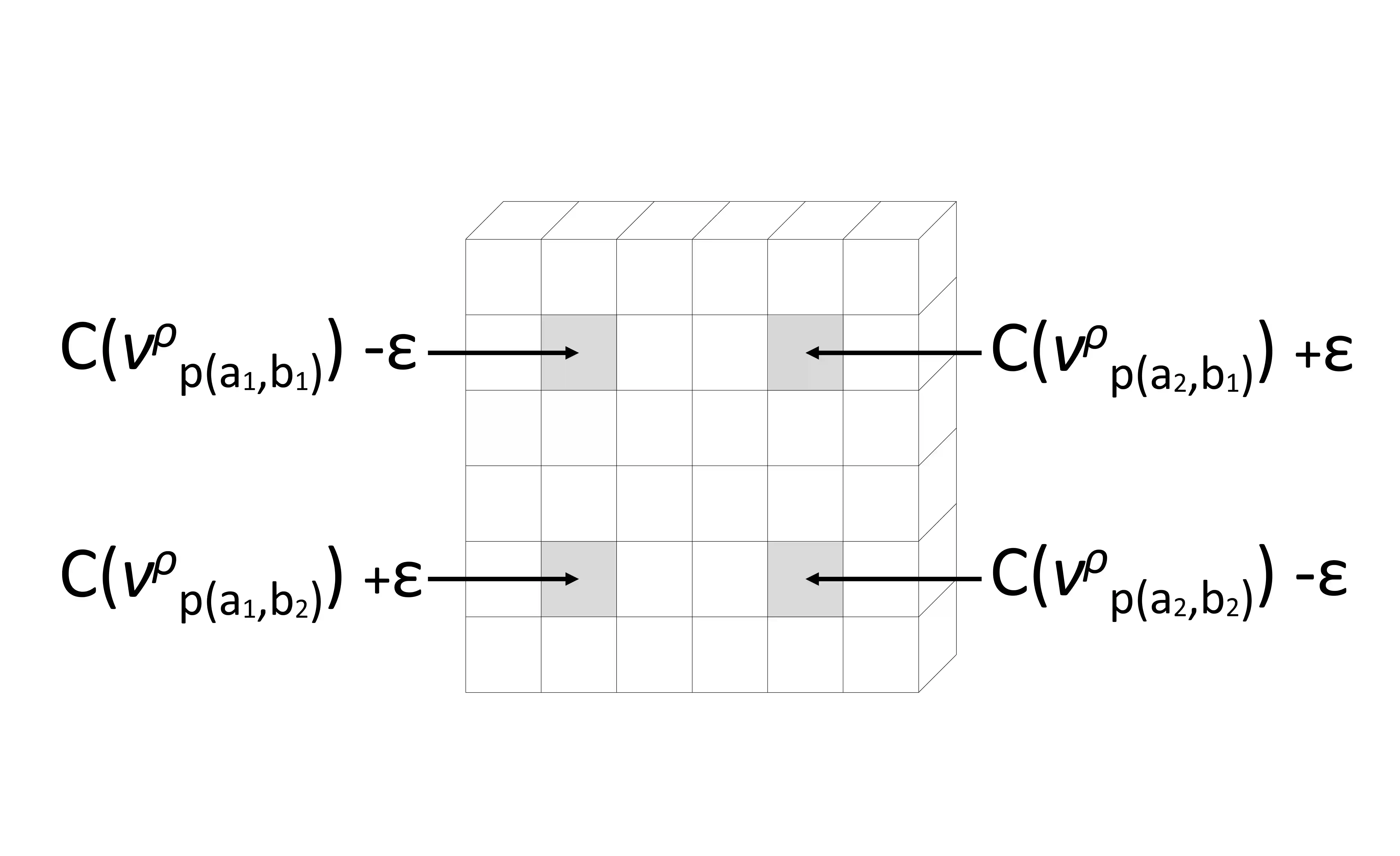
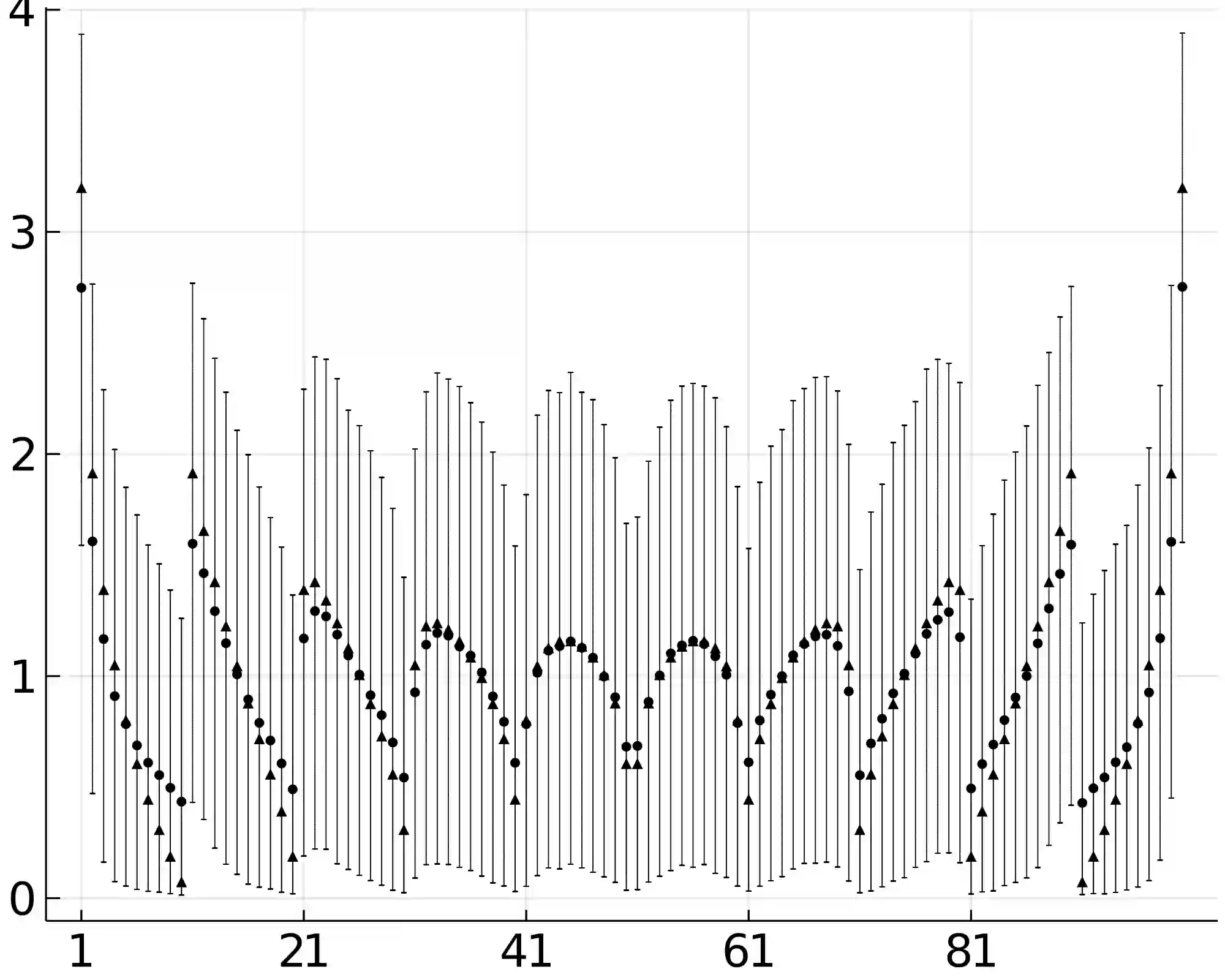
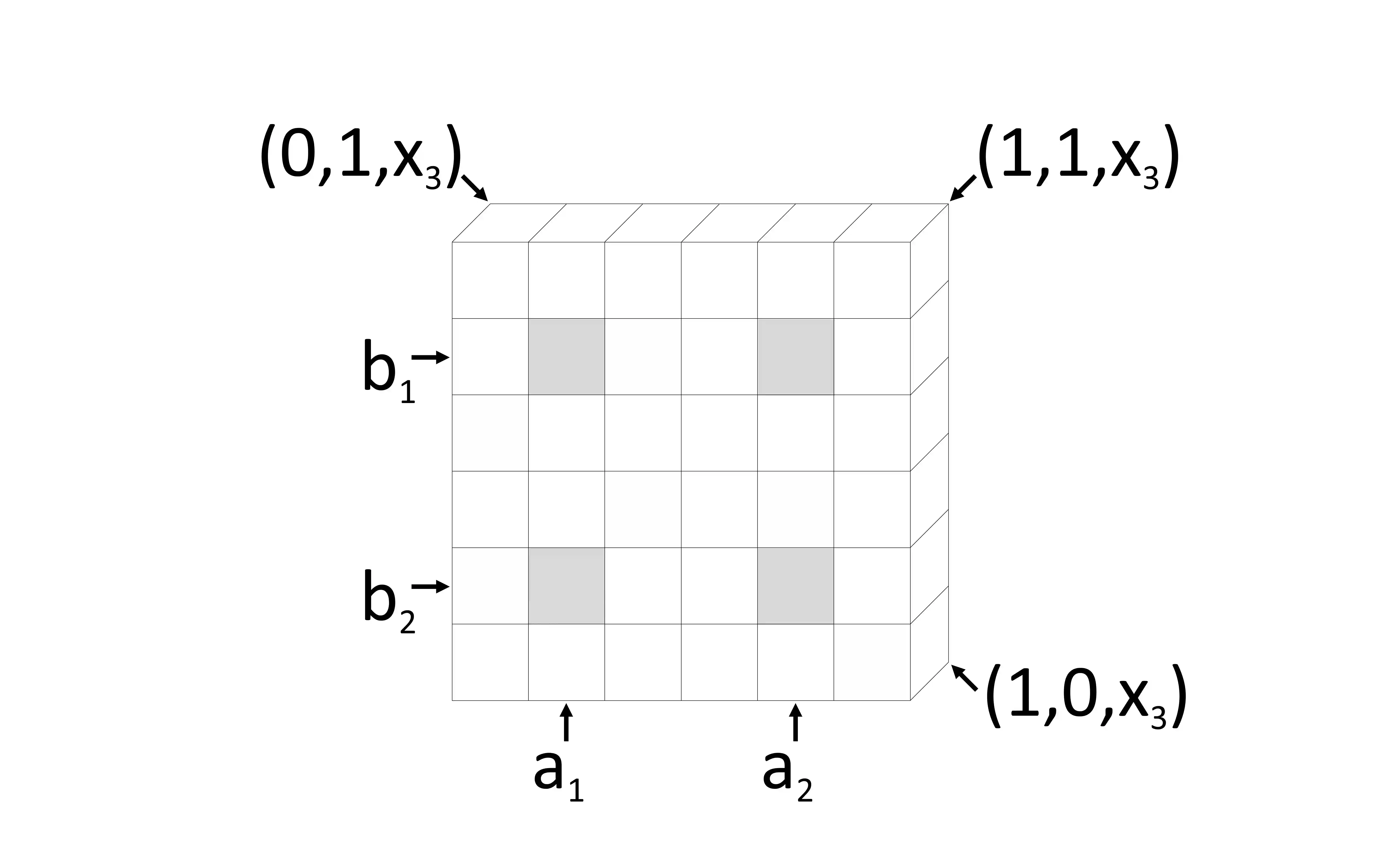Copula-based models provide a great deal of flexibility in modelling multivariate distributions, allowing for the specifications of models for the marginal distributions separately from the dependence structure (copula) that links them to form a joint distribution. Choosing a class of copula models is not a trivial task and its misspecification can lead to wrong conclusions. We introduce a novel class of grid-uniform copula functions, which is dense in the space of all continuous copula functions in a Hellinger sense. We propose a Bayesian model based on this class and develop an automatic Markov chain Monte Carlo algorithm for exploring the corresponding posterior distribution. The methodology is illustrated by means of simulated data and compared to the main existing approach.
翻译:以科普拉为基础的模型在模拟多变分布方面有很大的灵活性,使得边际分布模型的规格与依赖性结构(copula)分开,将其与形成联合分布(copula)联系起来。选择一类相近分配模型并非一项微不足道的任务,其分类错误可能导致错误的结论。我们引入了新型的网格-统一组合功能类别,该类别在Hellinger意义上所有连续相交功能的空间中十分密集。我们建议了一种基于此类的巴耶西亚模型,并开发了自动的Markov连锁Monte Carlo算法,用于探索相应的后方分布。该方法通过模拟数据与现有主要方法进行比较加以说明。