Inhomogeneous Markov Survival Regression Models

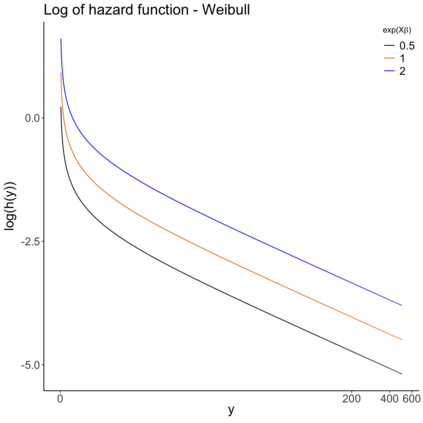
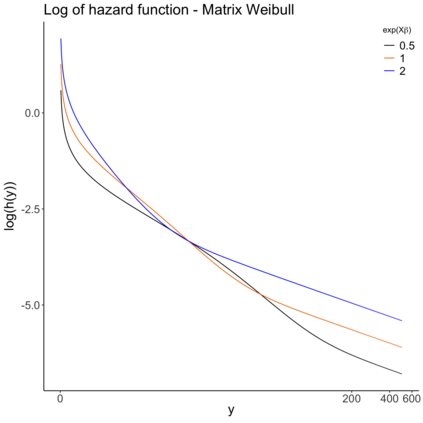
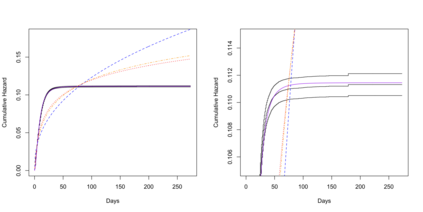
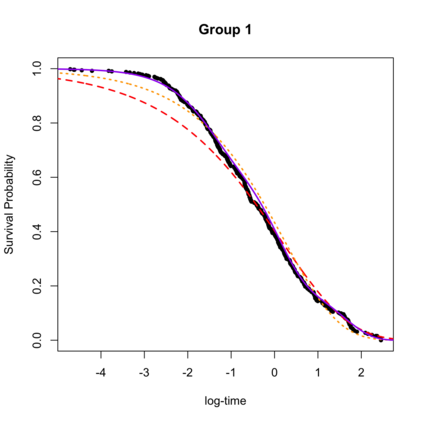
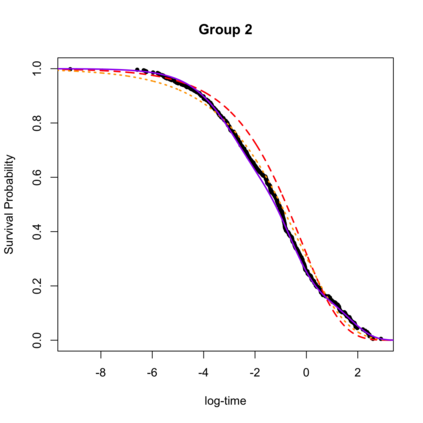
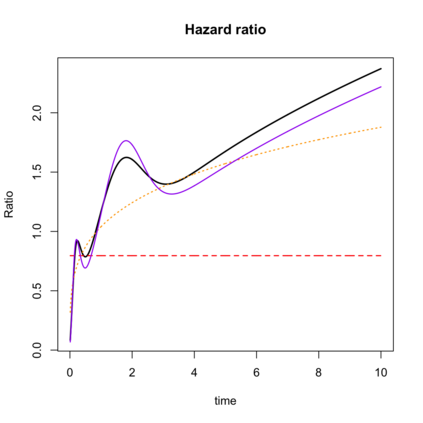
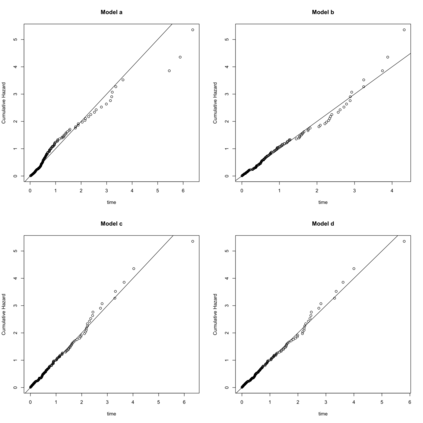
Regression models in survival analysis based on homogeneous and inhomogeneous phase-type distributions are proposed. The intensity function in this setting plays the role of the hazard function, having the additional benefit of being interpreted in terms of a hidden Markov structure. For unidimensional intensity matrices, we recover the proportional hazards and accelerated failure time models, among others. However, when considering higher dimensions, the proposed methods are only asymptotically equivalent to their classical counterparts and enjoy greater flexibility in the body of the distribution. For their estimation, the latent path representation of inhomogeneous Markov models is exploited. Consequently, an adapted EM algorithm is provided for which the likelihood increases at each iteration. Several examples of practical significance and relevant extensions are examined. The practical feasibility of the models is illustrated on simulated and real-world datasets.