GenEO coarse spaces for heterogeneous indefinite elliptic problems

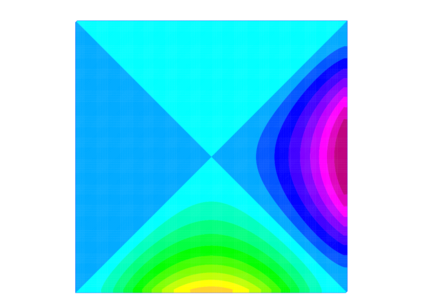
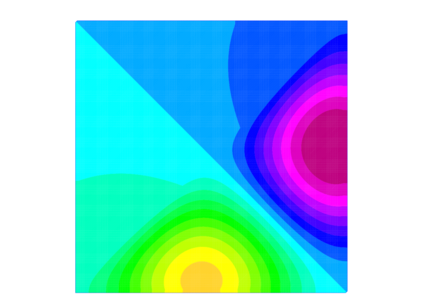
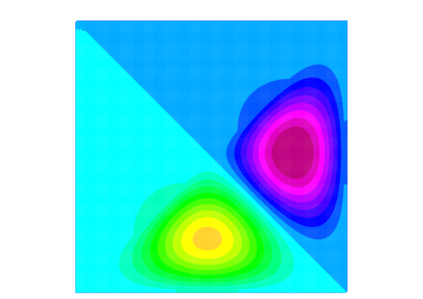
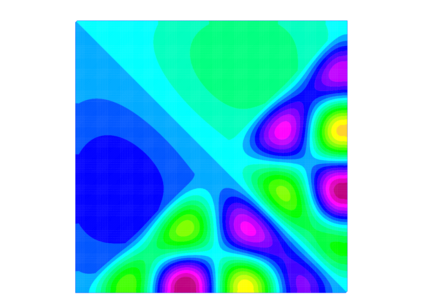
Motivated by recent work on coarse spaces for Helmholtz problems, we provide in this paper a comparative study on the use of spectral coarse spaces of GenEO type for heterogeneous indefinite elliptic problems within an additive overlapping Schwarz method. In particular, we focus here on two different but related formulations of local generalised eigenvalue problems and compare their performance numerically. Even though their behaviour seems to be very similar for several well-known heterogeneous test cases that are mildly indefinite, only one of the coarse spaces has so far been analysed theoretically, while the other one leads to a significantly more robust domain decomposition method when the indefiniteness is increased. We present a summary of upcoming results developing such a theory and describe how the numerical experiments illustrate it.