Time domain boundary integral equations and convolution quadrature for scattering by composite media (extended preprint)

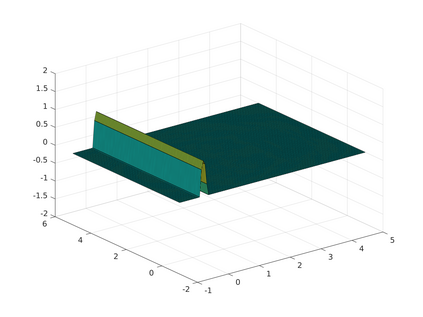
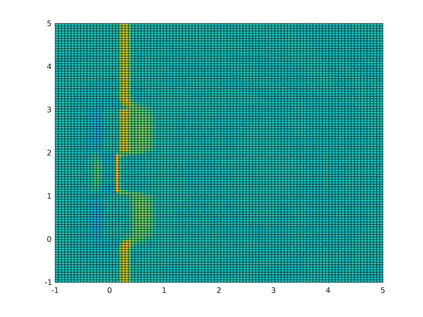
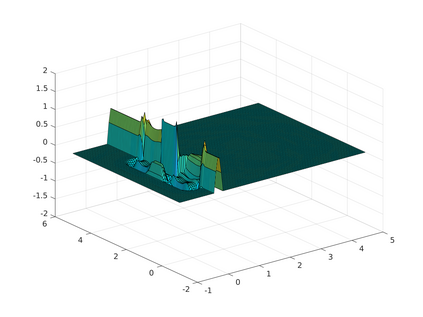
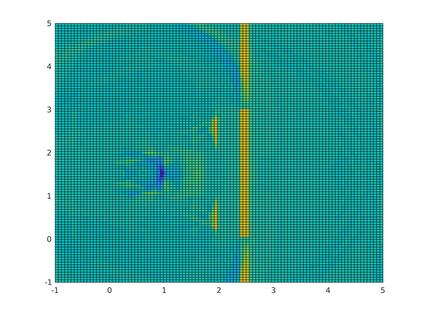
We consider acoustic scattering in heterogeneous media with piecewise constant wave number. The discretization is carried out using a Galerkin boundary element method in space and Runge-Kutta convolution quadrature in time. We prove well-posedness of the scheme and provide a priori estimates for the convergence in space and time.