On the Insufficiency of the Large Margins Theory in Explaining the Performance of Ensemble Methods

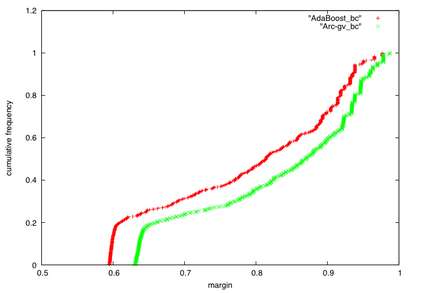
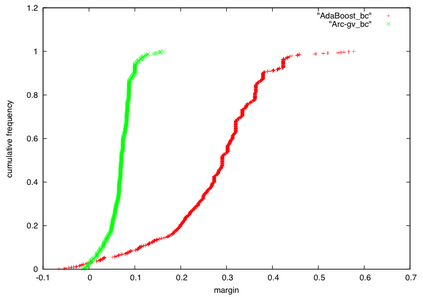
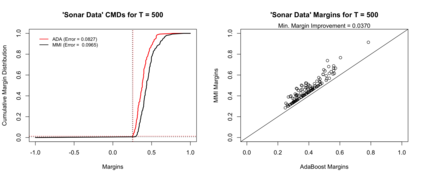
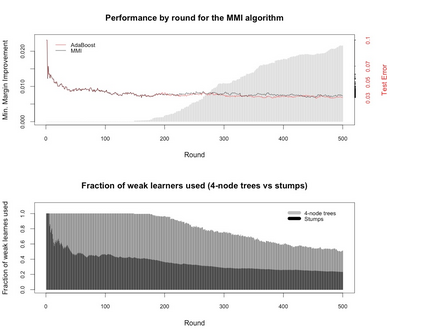
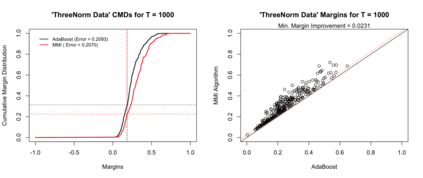
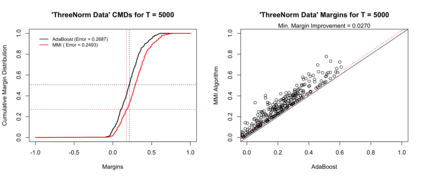
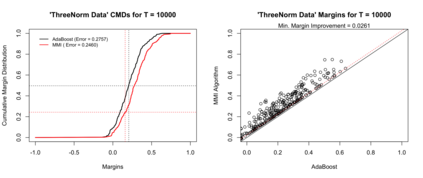
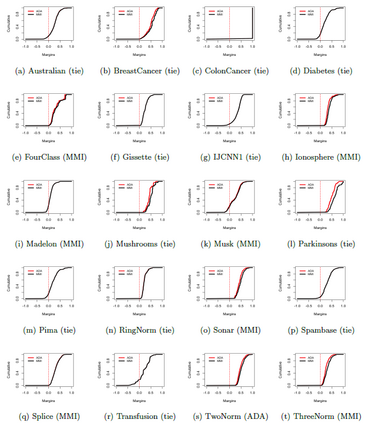
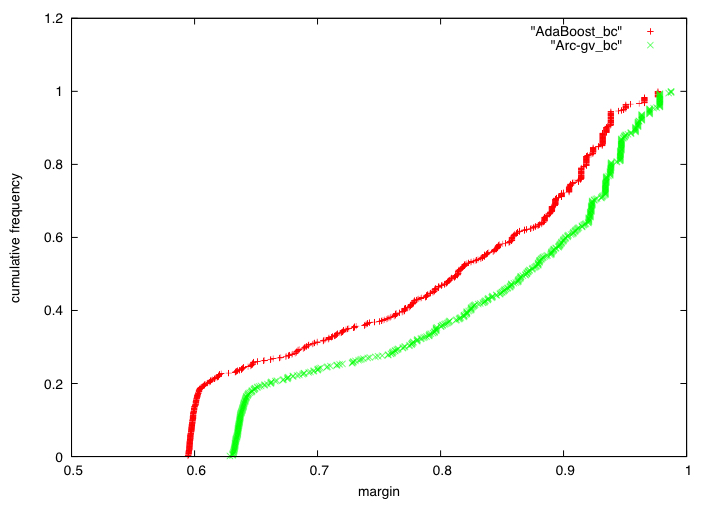
Boosting and other ensemble methods combine a large number of weak classifiers through weighted voting to produce stronger predictive models. To explain the successful performance of boosting algorithms, Schapire et al. (1998) showed that AdaBoost is especially effective at increasing the margins of the training data. Schapire et al. (1998) also developed an upper bound on the generalization error of any ensemble based on the margins of the training data, from which it was concluded that larger margins should lead to lower generalization error, everything else being equal (sometimes referred to as the ``large margins theory''). Tighter bounds have been derived and have reinforced the large margins theory hypothesis. For instance, Wang et al. (2011) suggest that specific margin instances, such as the equilibrium margin, can better summarize the margins distribution. These results have led many researchers to consider direct optimization of the margins to improve ensemble generalization error with mixed results. We show that the large margins theory is not sufficient for explaining the performance of voting classifiers. We do this by illustrating how it is possible to improve upon the margin distribution of an ensemble solution, while keeping the complexity fixed, yet not improve the test set performance.