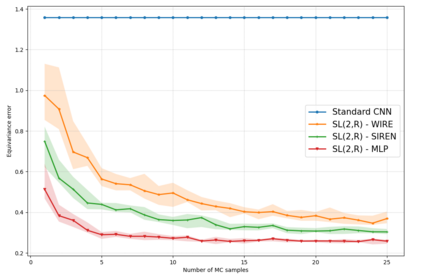
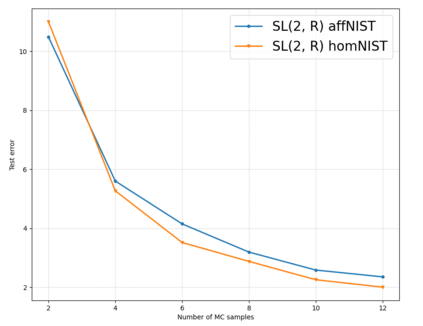
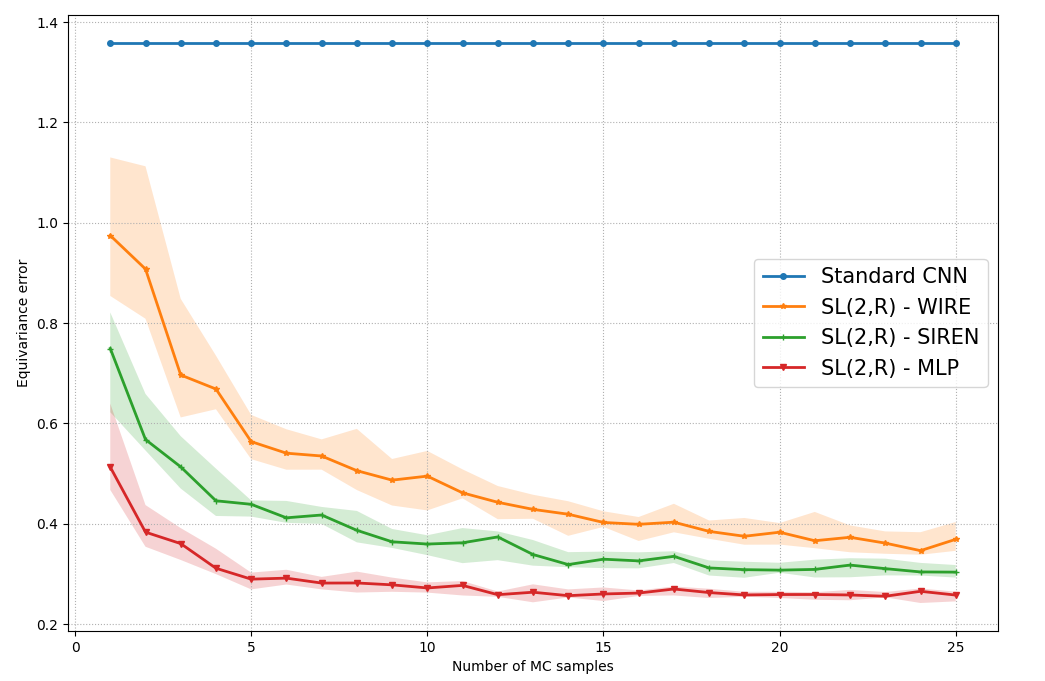
Invariance and equivariance to geometrical transformations have proven to be very useful inductive biases when training (convolutional) neural network models, especially in the low-data regime. Much work has focused on the case where the symmetry group employed is compact or abelian, or both. Recent work has explored enlarging the class of transformations used to the case of Lie groups, principally through the use of their Lie algebra, as well as the group exponential and logarithm maps. The applicability of such methods is limited by the fact that depending on the group of interest $G$, the exponential map may not be surjective. Further limitations are encountered when $G$ is neither compact nor abelian. Using the structure and geometry of Lie groups and their homogeneous spaces, we present a framework by which it is possible to work with such groups primarily focusing on the groups $G = \text{GL}^{+}(n, \mathbb{R})$ and $G = \text{SL}(n, \mathbb{R})$, as well as their representation as affine transformations $\mathbb{R}^{n} \rtimes G$. Invariant integration as well as a global parametrization is realized by a decomposition into subgroups and submanifolds which can be handled individually. Under this framework, we show how convolution kernels can be parametrized to build models equivariant with respect to affine transformations. We evaluate the robustness and out-of-distribution generalisation capability of our model on the benchmark affine-invariant classification task, outperforming previous proposals.
翻译:暂无翻译