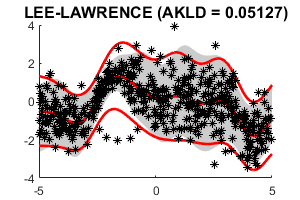
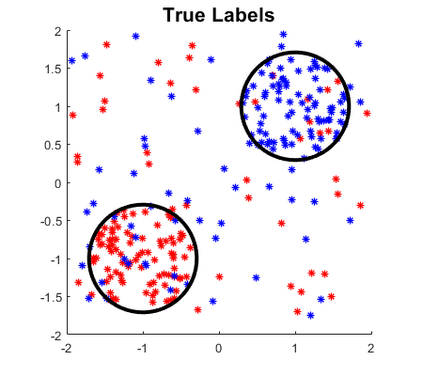
Despite the widespread utilization of Gaussian process models for versatile nonparametric modeling, they exhibit limitations in effectively capturing abrupt changes in function smoothness and accommodating relationships with heteroscedastic errors. Addressing these shortcomings, the heteroscedastic Gaussian process (HeGP) regression seeks to introduce flexibility by acknowledging the variability of residual variances across covariates in the regression model. In this work, we extend the HeGP concept, expanding its scope beyond regression tasks to encompass classification and state-space models. To achieve this, we propose a novel framework where the Gaussian process is coupled with a covariate-induced precision matrix process, adopting a mixture formulation. This approach enables the modeling of heteroscedastic covariance functions across covariates. To mitigate the computational challenges posed by sampling, we employ variational inference to approximate the posterior and facilitate posterior predictive modeling. Additionally, our training process leverages an EM algorithm featuring closed-form M-step updates to efficiently evaluate the heteroscedastic covariance function. A notable feature of our model is its consistent performance on multivariate responses, accommodating various types (continuous or categorical) seamlessly. Through a combination of simulations and real-world applications in climatology, we illustrate the model's prowess and advantages. By overcoming the limitations of traditional Gaussian process models, our proposed framework offers a robust and versatile tool for a wide array of applications.
翻译:暂无翻译