Algorithms for the Global Domination Problem

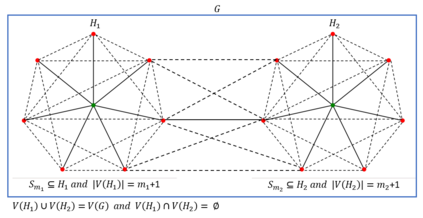
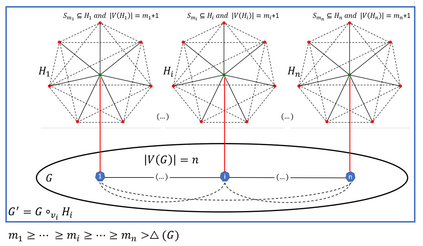
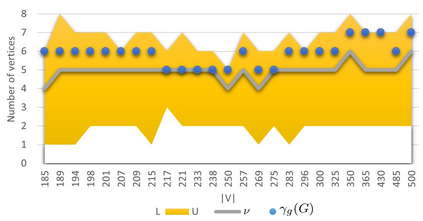
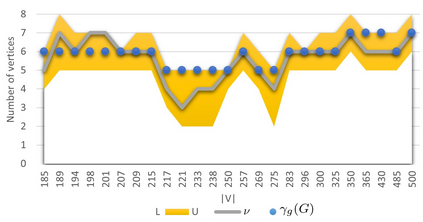
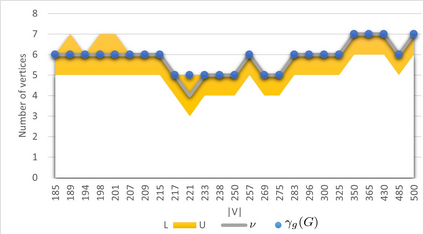
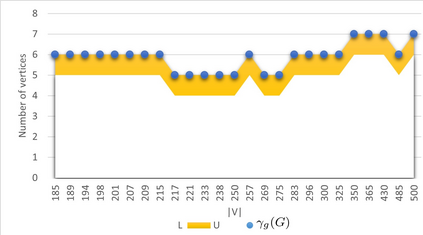
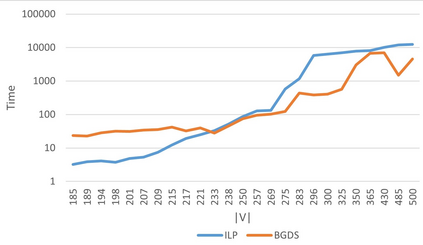
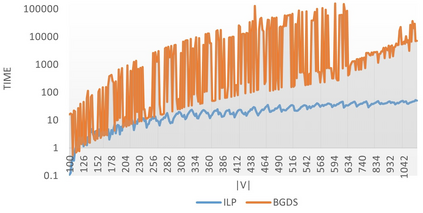
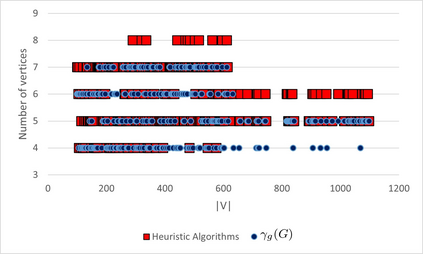
A dominating set D in a graph G is a subset of its vertices such that every vertex of the graph which does not belong to set D is adjacent to at least one vertex from set D. A set of vertices of graph G is a global dominating set if it is a dominating set for both, graph G and its complement. The objective is to find a global dominating set with the minimum cardinality. The problem is known to be NP-hard. Neither exact nor approximation algorithm existed . We propose two exact solution methods, one of them being based on an integer linear program (ILP) formulation, three heuristic algorithms and a special purification procedure that further reduces the size of a global dominated set delivered by any of our heuristic algorithms. We show that the problem remains NP-hard for restricted types of graphs and specify some families of graphs for which the heuristics guarantee the optimality. The second exact algorithm turned out to be about twice faster than ILP for graphs with more than 230 vertices and up to 1080 vertices, which were the largest benchmark instances that were solved optimally. The heuristics were tested for the existing 2284 benchmark problem instances with up to 14000 vertices and delivered solutions for the largest instances in less than one minute. Remarkably, for about 52% of the 1000 instances with the obtained optimal solutions, at least one of the heuristics generated an optimal solution, where the average approximation error for the remaining instances was 1.07%.