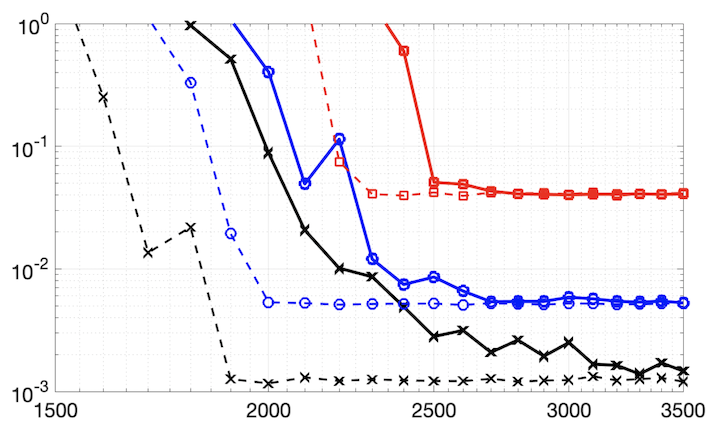
The learning speed of feed-forward neural networks is notoriously slow and has presented a bottleneck in deep learning applications for several decades. For instance, gradient-based learning algorithms, which are used extensively to train neural networks, tend to work slowly when all of the network parameters must be iteratively tuned. To counter this, both researchers and practitioners have tried introducing randomness to reduce the learning requirement. Based on the original construction of Igelnik and Pao, single layer neural-networks with random input-to-hidden layer weights and biases have seen success in practice, but the necessary theoretical justification is lacking. In this paper, we begin to fill this theoretical gap. We provide a (corrected) rigorous proof that the Igelnik and Pao construction is a universal approximator for continuous functions on compact domains, with approximation error decaying asymptotically like $O(1/\sqrt{n})$ for the number $n$ of network nodes. We then extend this result to the non-asymptotic setting, proving that one can achieve any desired approximation error with high probability provided $n$ is sufficiently large. We further adapt this randomized neural network architecture to approximate functions on smooth, compact submanifolds of Euclidean space, providing theoretical guarantees in both the asymptotic and non-asymptotic forms. Finally, we illustrate our results on manifolds with numerical experiments.
翻译:向向神经网络进料的学习速度非常缓慢,而且数十年来在深层学习应用中都出现了瓶颈。例如,基于梯度的学习算法,广泛用于培养神经网络,当所有网络参数必须迭接时,这种算法往往会缓慢工作。对此,研究人员和从业人员都试图采用随机性来减少学习要求。根据最初建造的Igelnik和Pao, 单层神经网络以随机输入到隐藏层重量和偏差,在实践上取得了成功,但缺乏必要的理论理由。在本文中,我们开始填补这一理论差距。我们提供了(经校正的)严格证据,证明Igelnik和Pao建筑是所有网络连续功能的通用近似近似误差,无症状地腐蚀了网络节点的美元。我们随后将这一结果推广到非抽查的设置中,证明我们能够以高概率提供任何理想的近似近似近似近似误差的Eqoloral colorizal commal oral room room room room room room room room room room room roupal dal droupl droupl droom 提供足够充分的功能。