A local MCMC algorithm for variable selection with dimension-free mixing time

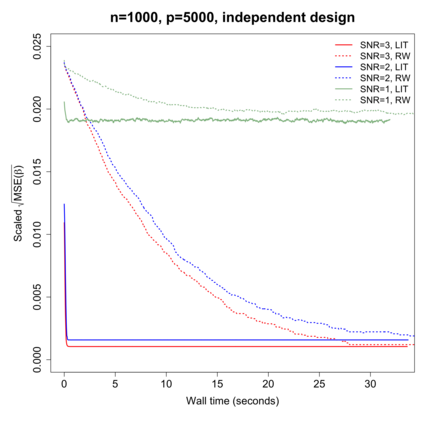
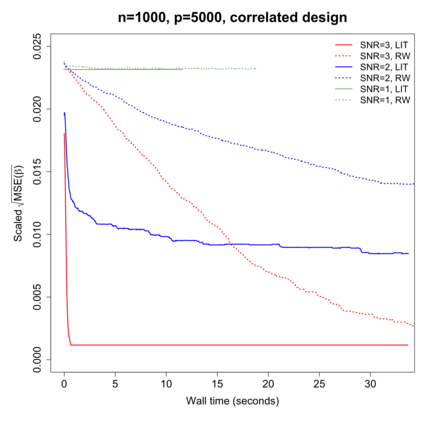
Yang et al. (2016) proved that the symmetric random walk Metropolis--Hastings algorithm for Bayesian variable selection is rapidly mixing under mild high-dimensional assumptions. In this work, we introduce a novel Metropolis--Hastings algorithm, which still proposes new states via add-delete-swap moves but has a much faster mixing time independent of the number of covariates. The key idea is to use a locally informed proposal scheme with bounded weights. Motivated by the theoretical analysis of our algorithm, we further propose a method called "two-stage drift condition" for studying convergence rates of Markov chains on general state spaces. Simulation studies show that the new algorithm can efficiently explore the posterior distribution under various settings. A real data example is also provided, where five genetic variants associated with cup-to-disk ratio are identified.