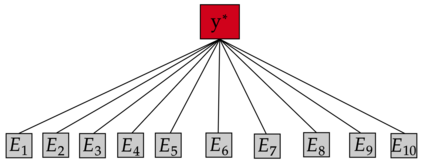
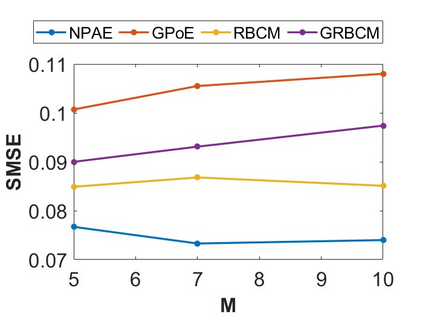
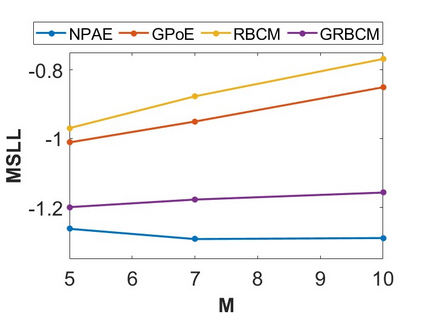
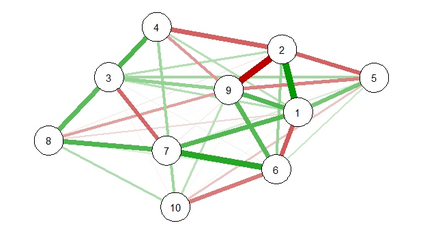
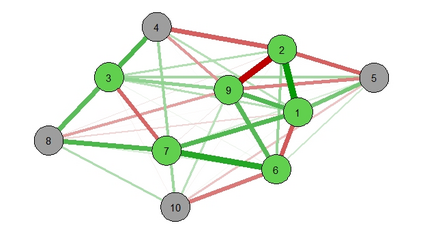
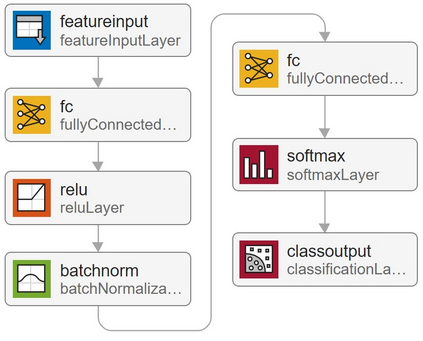
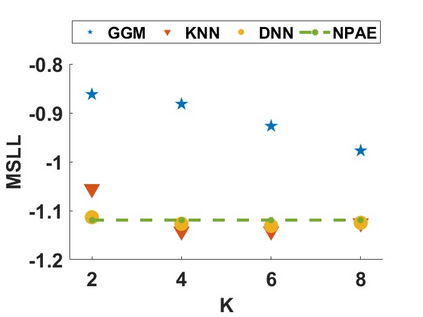
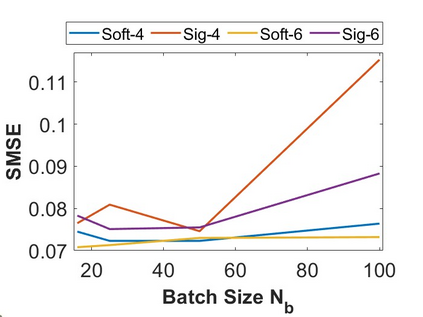
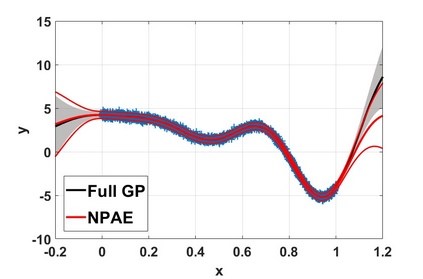
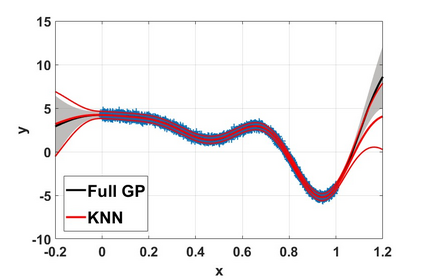
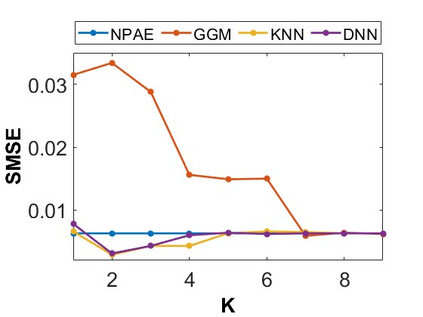
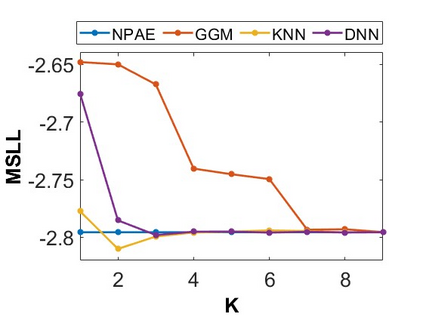
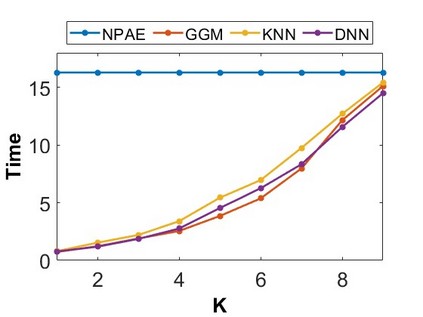
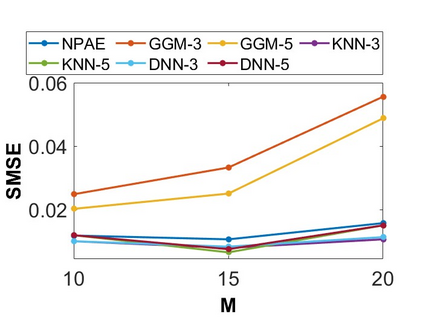
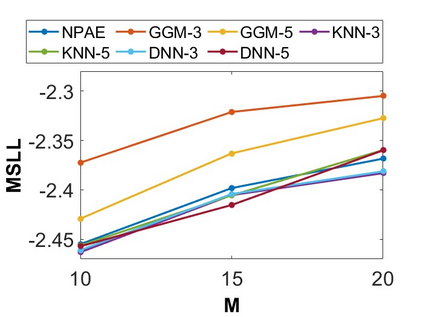
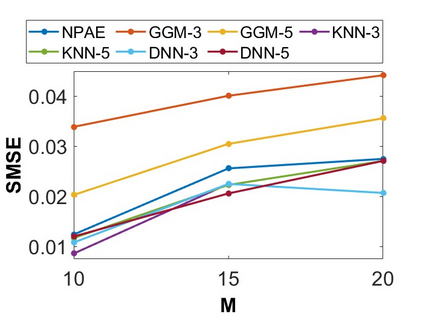
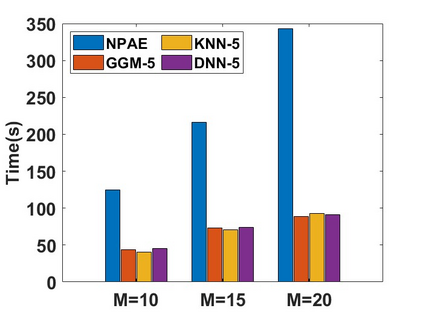
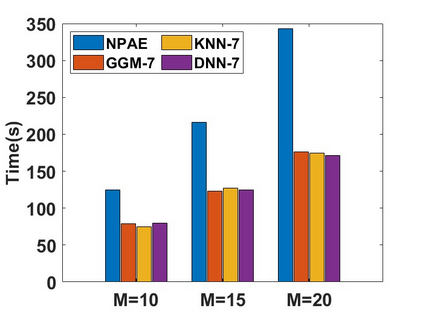
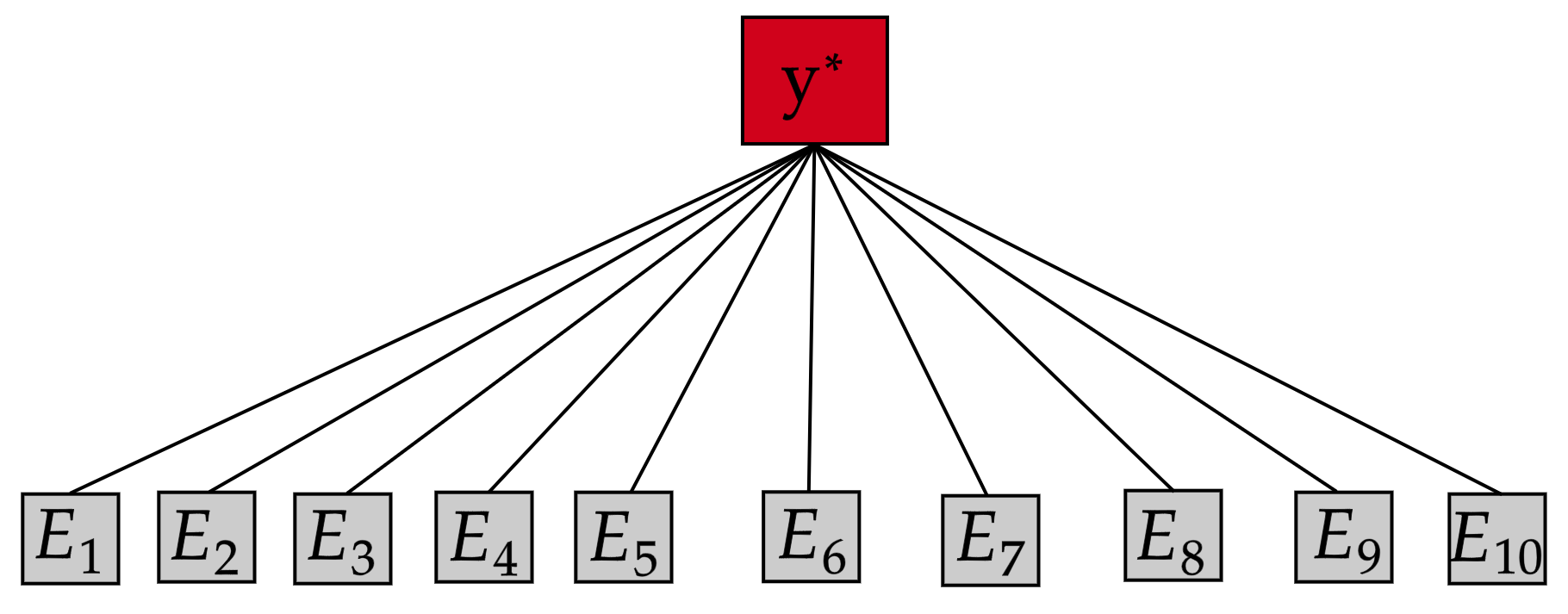
By distributing the training process, local approximation reduces the cost of the standard Gaussian Process. An ensemble technique combines local predictions from Gaussian experts trained on different partitions of the data. Ensemble methods aggregate models' predictions by assuming a perfect diversity of local predictors. Although it keeps the aggregation tractable, this assumption is often violated in practice. Even though ensemble methods provide consistent results by assuming dependencies between experts, they have a high computational cost, which is cubic in the number of experts involved. By implementing an expert selection strategy, the final aggregation step uses fewer experts and is more efficient. However, a selection approach that assigns a fixed set of experts to each new data point cannot encode the specific properties of each unique data point. This paper proposes a flexible expert selection approach based on the characteristics of entry data points. To this end, we investigate the selection task as a multi-label classification problem where the experts define labels, and each entry point is assigned to some experts. The proposed solution's prediction quality, efficiency, and asymptotic properties are discussed in detail. We demonstrate the efficacy of our method through extensive numerical experiments using synthetic and real-world data sets.
翻译:暂无翻译