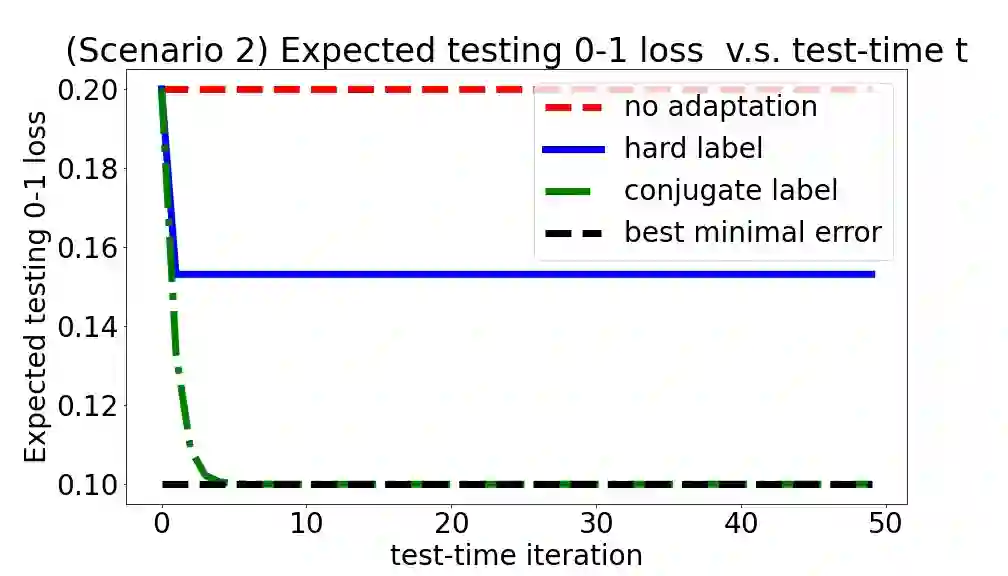
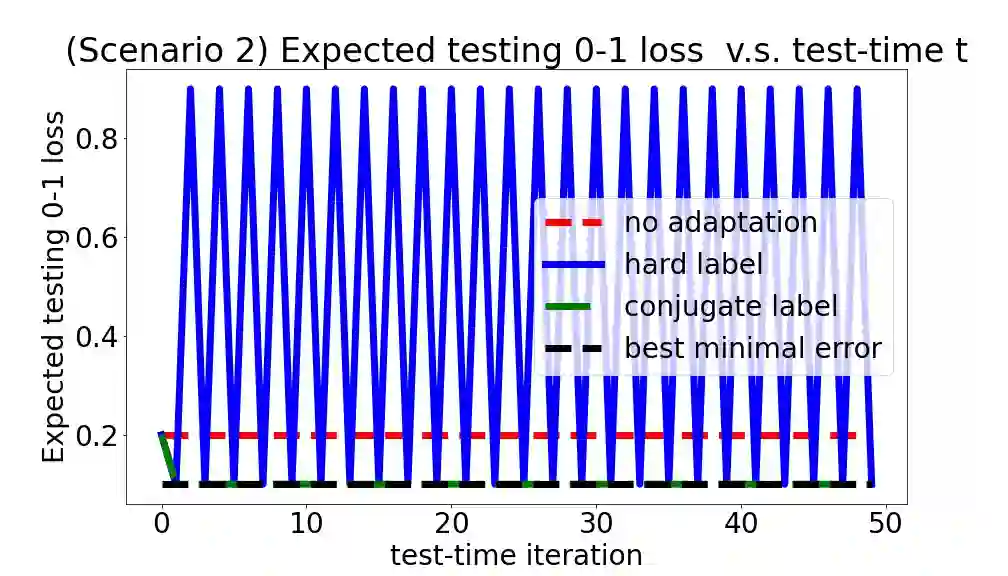
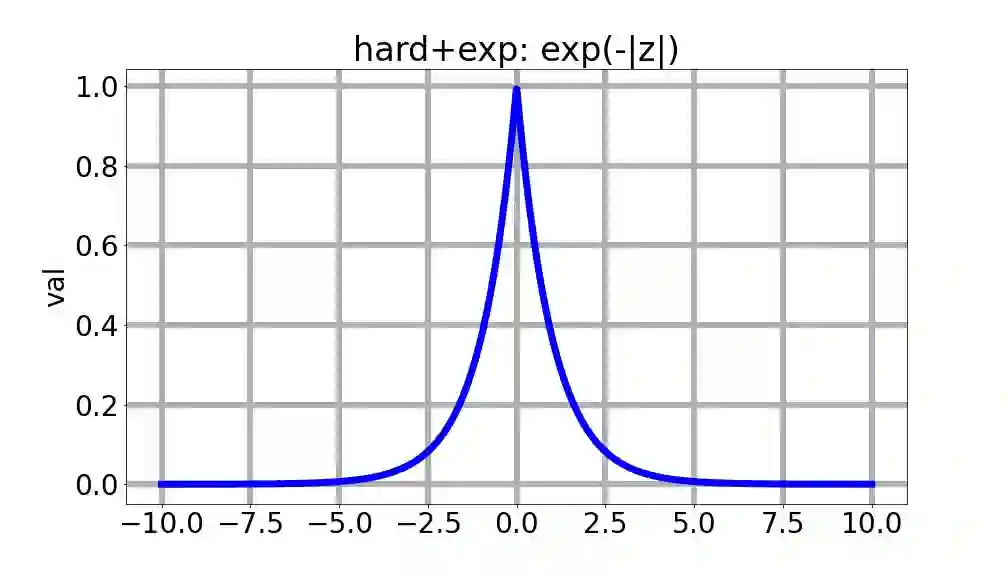
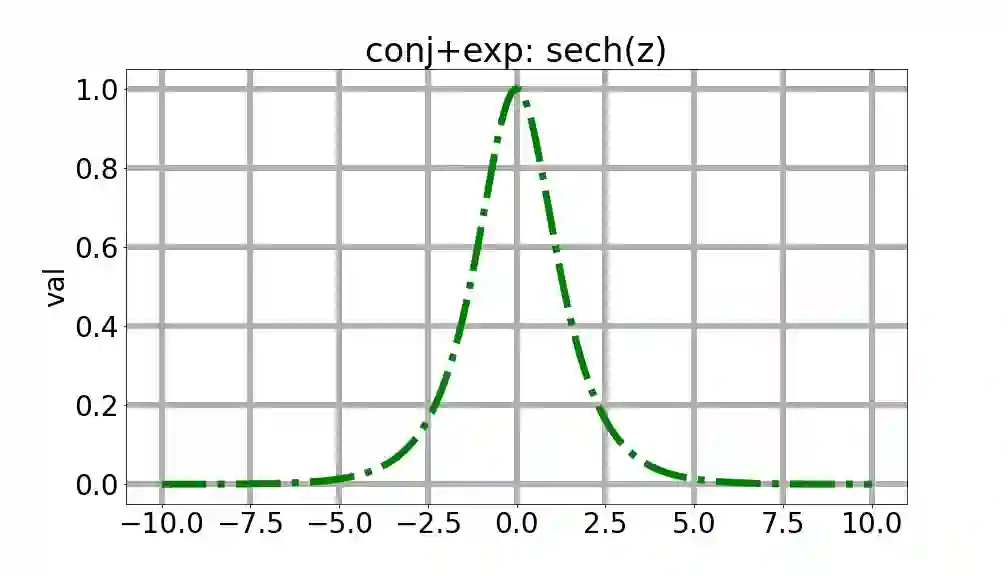
We consider a setting that a model needs to adapt to a new domain under distribution shifts, given that only unlabeled test samples from the new domain are accessible at test time. A common idea in most of the related works is constructing pseudo-labels for the unlabeled test samples and applying gradient descent (GD) to a loss function with the pseudo-labels. Recently, Goyal et al. (2022) propose conjugate labels, which is a new kind of pseudo-labels for self-training at test time. They empirically show that the conjugate label outperforms other ways of pseudo-labeling on many domain adaptation benchmarks. However, provably showing that GD with conjugate labels learns a good classifier for test-time adaptation remains open. In this work, we aim at theoretically understanding GD with hard and conjugate labels for a binary classification problem. We show that for square loss, GD with conjugate labels converges to a solution that minimizes the testing 0-1 loss under a Gaussian model, while GD with hard pseudo-labels fails in this task. We also analyze them under different loss functions for the update. Our results shed lights on understanding when and why GD with hard labels or conjugate labels works in test-time adaptation.
翻译:我们认为一个模型需要适应分布变换下的新域的设置, 因为在测试时, 只有新域的未贴标签测试样本才能进入新的域块。 大多数相关工程的共同理念是为未贴标签的试样建立假标签, 并将梯度下降( GD) 应用于假标签的损失函数。 最近, Goyal 等人( 2022) 提出了同级标签, 这是测试时用于自我培训的一种新型假标签。 它们的经验显示, 共标标签比其他伪标签方法要优于许多域域适应基准上的假标签。 然而, 相关工程的一个常见想法是, 为未贴标签的试样样本制作假标签的GD 学习一个良好的分类器, 并将梯度下降( GG) 应用到一个假标签上。 我们的目标是从理论上去理解GD, 硬标签标签上的同级标签。 我们用同级标签上的GD 标签会集中到一个解决方案, 将测试0-1损失降到最小, 而 GD 则用硬质标签在任务上更新结果。