Implicit Regularization in ReLU Networks with the Square Loss

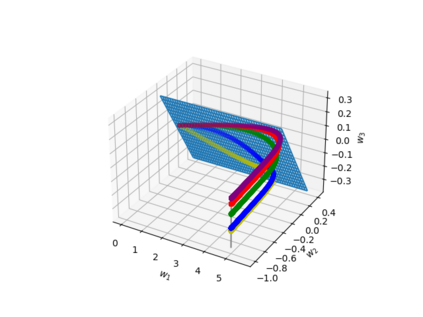
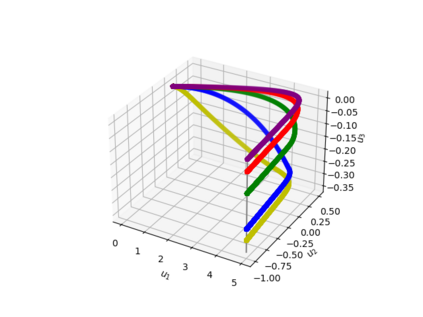
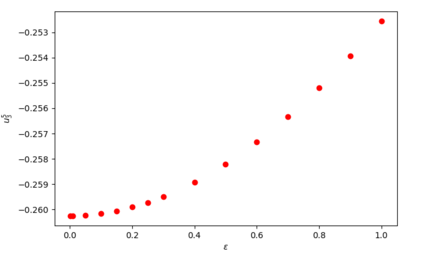
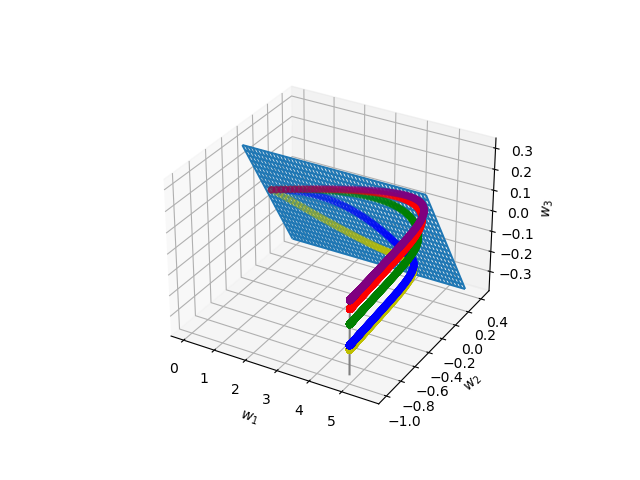
Understanding the implicit regularization (or implicit bias) of gradient descent has recently been a very active research area. However, the implicit regularization in nonlinear neural networks is still poorly understood, especially for regression losses such as the square loss. Perhaps surprisingly, we prove that even for a single ReLU neuron, it is \emph{impossible} to characterize the implicit regularization with the square loss by any explicit function of the model parameters (although on the positive side, we show it can be characterized approximately). For one hidden-layer networks, we prove a similar result, where in general it is impossible to characterize implicit regularization properties in this manner, \emph{except} for the "balancedness" property identified in Du et al. [2018]. Our results suggest that a more general framework than the one considered so far may be needed to understand implicit regularization for nonlinear predictors, and provides some clues on what this framework should be.