Analysis and algorithms for $\ell_p$-based semi-supervised learning on graphs

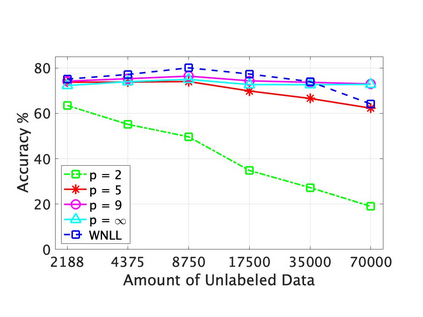
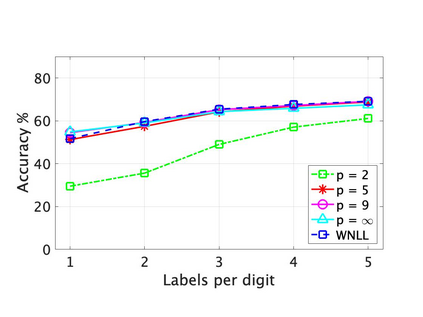
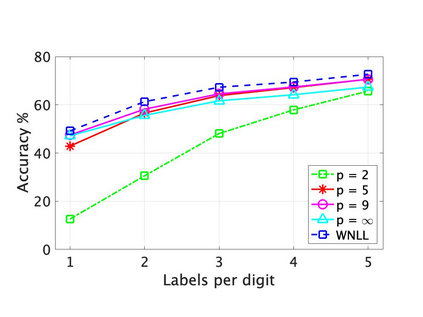
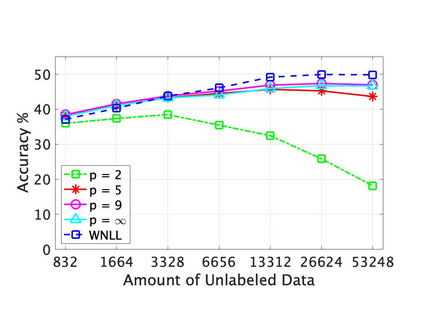
This paper addresses theory and applications of $\ell_p$-based Laplacian regularization in semi-supervised learning. The graph $p$-Laplacian for $p>2$ has been proposed recently as a replacement for the standard ($p=2$) graph Laplacian in semi-supervised learning problems with very few labels, where Laplacian learning is degenerate. In the first part of the paper we prove new discrete to continuum convergence results for $p$-Laplace problems on $k$-nearest neighbor ($k$-NN) graphs, which are more commonly used in practice than random geometric graphs. Our analysis shows that, on $k$-NN graphs, the $p$-Laplacian retains information about the data distribution as $p\to \infty$ and Lipschitz learning ($p=\infty$) is sensitive to the data distribution. This situation can be contrasted with random geometric graphs, where the $p$-Laplacian forgets the data distribution as $p\to \infty$. We also present a general framework for proving discrete to continuum convergence results in graph-based learning that only requires pointwise consistency and monotonicity. In the second part of the paper, we develop fast algorithms for solving the variational and game-theoretic $p$-Laplace equations on weighted graphs for $p>2$. We present several efficient and scalable algorithms for both formulations, and present numerical results on synthetic data indicating their convergence properties. Finally, we conduct extensive numerical experiments on the MNIST, FashionMNIST and EMNIST datasets that illustrate the effectiveness of the $p$-Laplacian formulation for semi-supervised learning with few labels. In particular, we find that Lipschitz learning ($p=\infty$) performs well with very few labels on $k$-NN graphs, which experimentally validates our theoretical findings that Lipschitz learning retains information about the data distribution (the unlabeled data) on $k$-NN graphs.