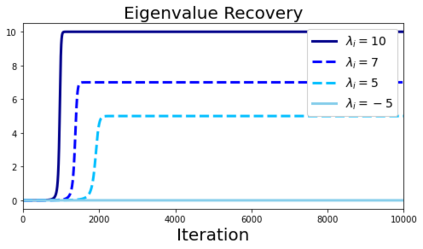
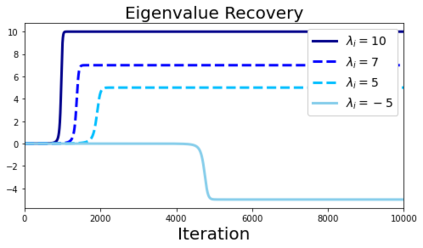
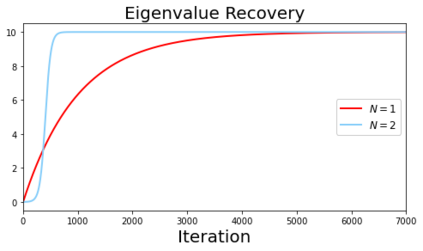
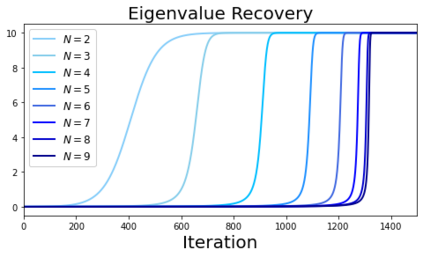
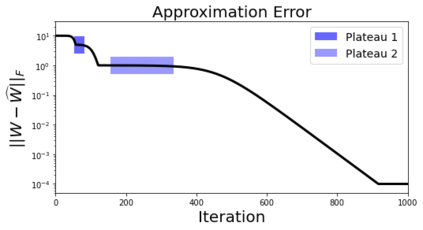
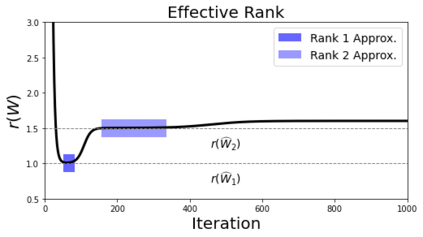
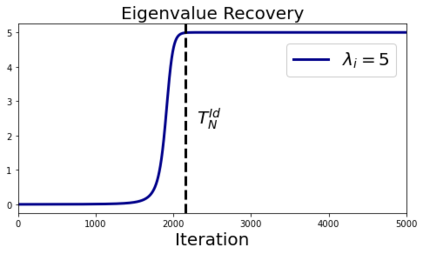
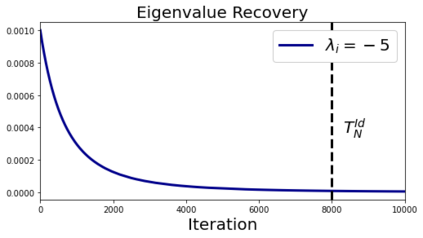
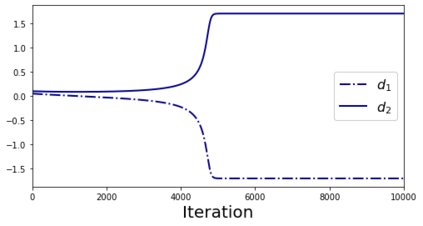
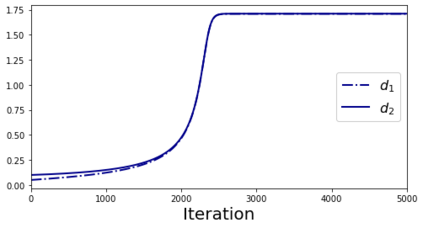
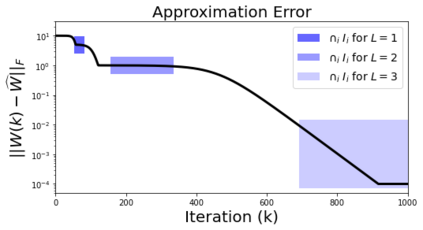
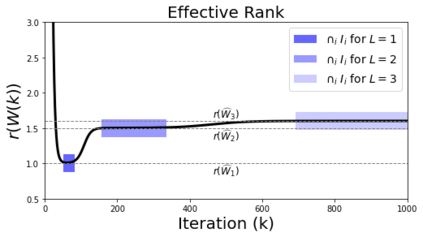
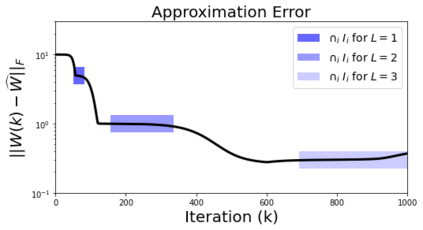
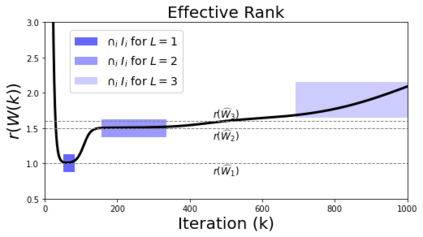
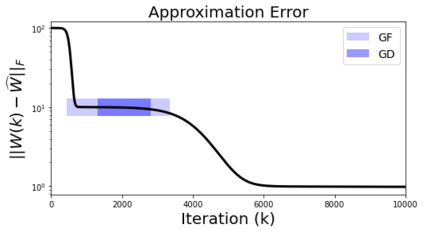
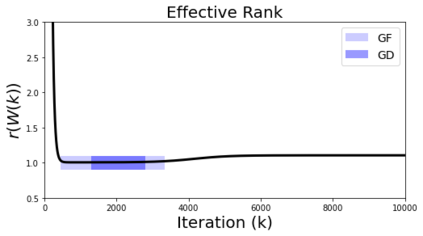
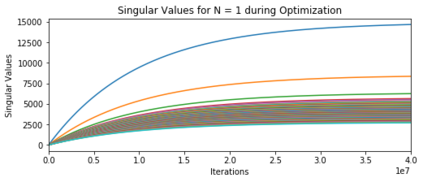
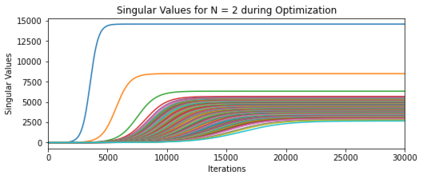
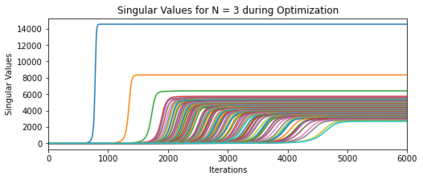
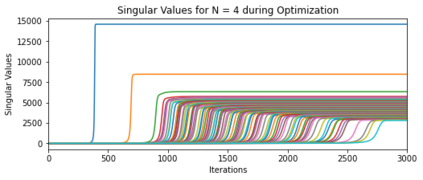
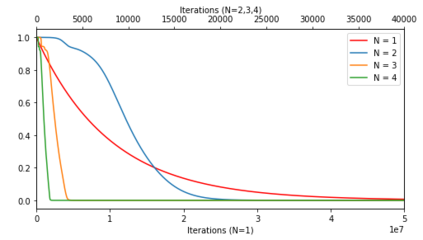
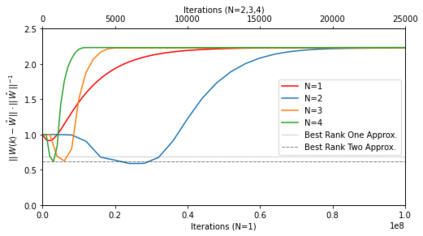
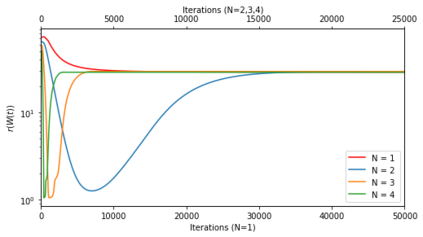
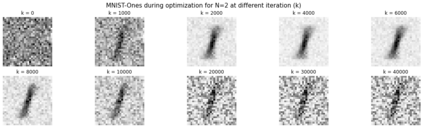
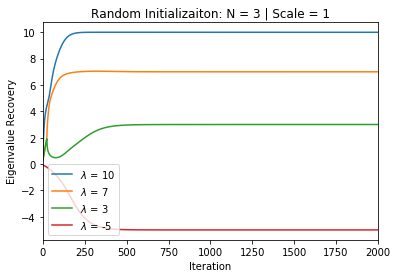
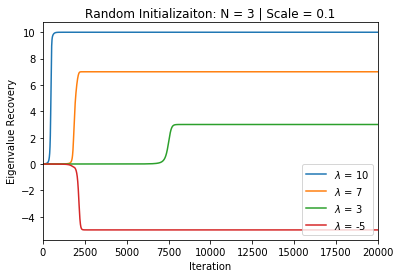
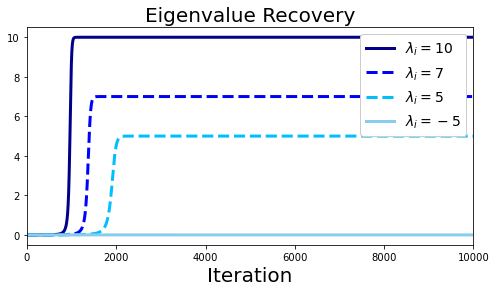
In deep learning, it is common to use more network parameters than training points. In such scenarioof over-parameterization, there are usually multiple networks that achieve zero training error so that thetraining algorithm induces an implicit bias on the computed solution. In practice, (stochastic) gradientdescent tends to prefer solutions which generalize well, which provides a possible explanation of thesuccess of deep learning. In this paper we analyze the dynamics of gradient descent in the simplifiedsetting of linear networks and of an estimation problem. Although we are not in an overparameterizedscenario, our analysis nevertheless provides insights into the phenomenon of implicit bias. In fact, wederive a rigorous analysis of the dynamics of vanilla gradient descent, and characterize the dynamicalconvergence of the spectrum. We are able to accurately locate time intervals where the effective rankof the iterates is close to the effective rank of a low-rank projection of the ground-truth matrix. Inpractice, those intervals can be used as criteria for early stopping if a certain regularity is desired. Wealso provide empirical evidence for implicit bias in more general scenarios, such as matrix sensing andrandom initialization. This suggests that deep learning prefers trajectories whose complexity (measuredin terms of effective rank) is monotonically increasing, which we believe is a fundamental concept for thetheoretical understanding of deep learning.
翻译:在深层学习中,通常使用比培训点更多的网络参数。在这种超度参数化的假设中,通常存在多个网络,实现零培训错误,使培训算法在计算解决方案上产生隐含的偏差。在实践中,(随机的)梯度偏向偏向于概括性的解决办法,这为深层学习的成败提供了可能的解释。在本文中,我们分析在简化线性网络的设置和估计问题方面梯度下降的动态。虽然我们没有处于过分分度化的假设中,但我们的分析却提供了对隐性偏差现象的洞察力。事实上,对香草梯度下降的动态进行严谨分析,并描述频谱的动态趋同特征。我们能够准确地定位时间间隔,以便准确定位其有效水平接近于低水平的地面图表预测的有效等级。实践是,如果需要某种规律性,这些间隔可以用作早期停止的标准。我们还提供了在更普遍的假设中隐藏的偏向性偏向性偏向,例如矩阵感测深的深度测深度和深度测深度概念,从而相信这种测深的深度测深的深度测深度是核心的测测测度,这种测地测测测度是基础。