Approximate Fixed-Points in Recurrent Neural Networks

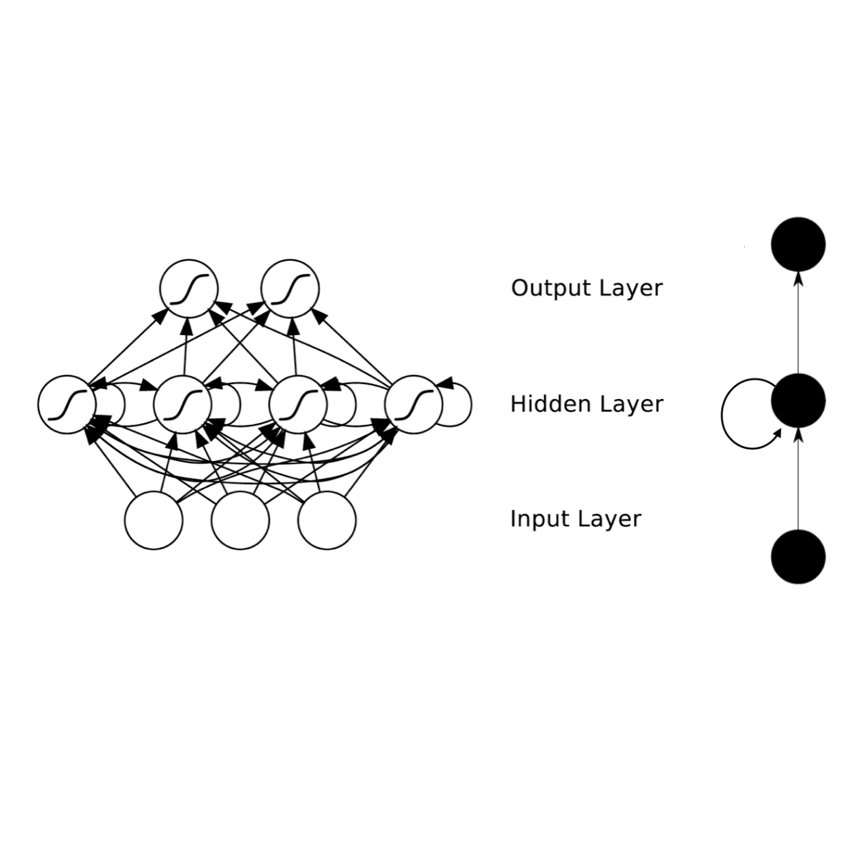
Recurrent neural networks are widely used in speech and language processing. Due to dependency on the past, standard algorithms for training these models, such as back-propagation through time (BPTT), cannot be efficiently parallelised. Furthermore, applying these models to more complex structures than sequences requires inference time approximations, which introduce inconsistency between inference and training. This paper shows that recurrent neural networks can be reformulated as fixed-points of non-linear equation systems. These fixed-points can be computed using an iterative algorithm exactly and in as many iterations as the length of any given sequence. Each iteration of this algorithm adds one additional Markovian-like order of dependencies such that upon termination all dependencies modelled by the recurrent neural networks have been incorporated. Although exact fixed-points inherit the same parallelization and inconsistency issues, this paper shows that approximate fixed-points can be computed in parallel and used consistently in training and inference including tasks such as lattice rescoring. Experimental validation is performed in two tasks, Penn Tree Bank and WikiText-2, and shows that approximate fixed-points yield competitive prediction performance to recurrent neural networks trained using the BPTT algorithm.