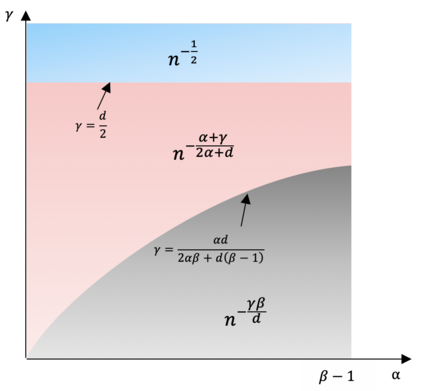
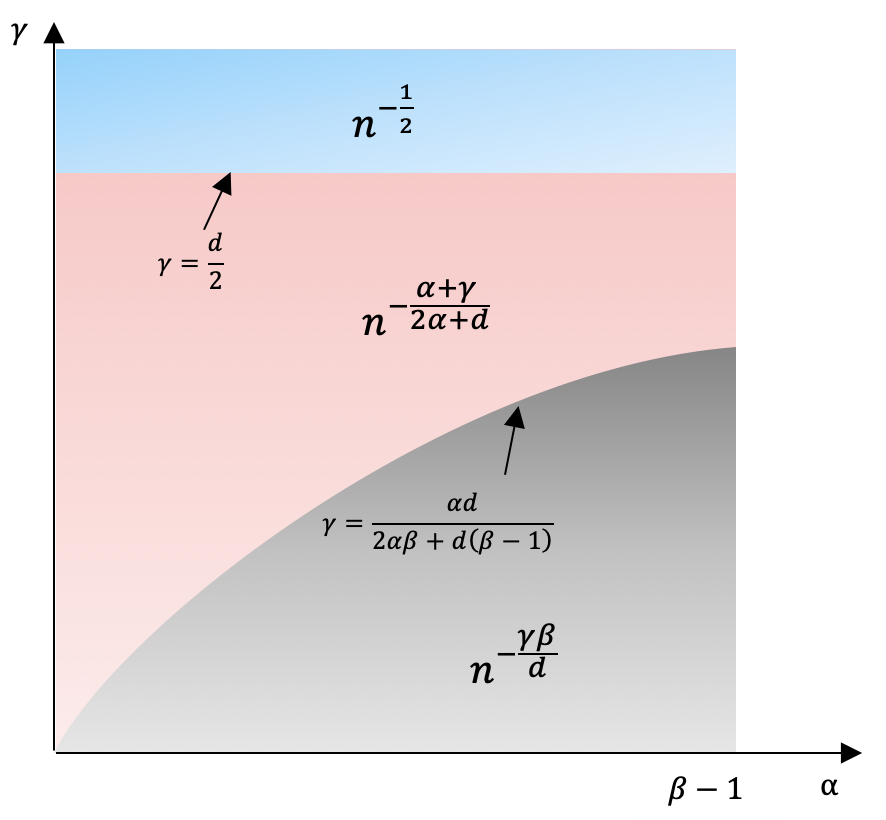
Statistical inference from high-dimensional data with low-dimensional structures has recently attracted lots of attention. In machine learning, deep generative modeling approaches implicitly estimate distributions of complex objects by creating new samples from the underlying distribution, and have achieved great success in generating synthetic realistic-looking images and texts. A key step in these approaches is the extraction of latent features or representations (encoding) that can be used for accurately reconstructing the original data (decoding). In other words, low-dimensional manifold structure is implicitly assumed and utilized in the distribution modeling and estimation. To understand the benefit of low-dimensional manifold structure in generative modeling, we build a general minimax framework for distribution estimation on unknown submanifold under adversarial losses, with suitable smoothness assumptions on the target distribution and the manifold. The established minimax rate elucidates how various problem characteristics, including intrinsic dimensionality of the data and smoothness levels of the target distribution and the manifold, affect the fundamental limit of high-dimensional distribution estimation. To prove the minimax upper bound, we construct an estimator based on a mixture of locally fitted generative models, which is motivated by the partition of unity technique from differential geometry and is necessary to cover cases where the underlying data manifold does not admit a global parametrization. We also propose a data-driven adaptive estimator that is shown to simultaneously attain within a logarithmic factor of the optimal rate over a large collection of distribution classes.
翻译:在机器学习中,深基因模型方法通过从基本分布中创建新的样本,暗含地估计复杂物体的分布,通过从基本分布中创建新的样本,在制作合成现实的图像和文本方面取得巨大成功。这些方法的一个关键步骤是提取可用于准确重建原始数据(解码)的潜在特征或表示(编码),换句话说,在分布模型和估计中暗含地假设和使用低维多元结构。为了了解基因模型中低维多元结构的好处,我们为在对抗性损失中对未知亚拼图进行分布估计建立了一个一般微缩框架,对目标分布和方位作了适当的平稳假设。既定的微缩缩缩率说明了各种问题特征是如何影响原始数据(数据分布和元件的内在维度和平稳度)的。为了证明微缩多维度分布估计的基本限度,我们根据当地适应性基因模型的混合,建立了一个总的微缩缩缩缩图框架,用于估算在对抗性损失中未知的亚拼图下对不明次次次的分布,同时假设在目标分布和方位数分布和方位数的假设方面,我们从一个不具有动力的深度的深度分析基础,因此从全球数据收集和深度分析中选择了一种大比例,从一个不具有动力地标定的模型。