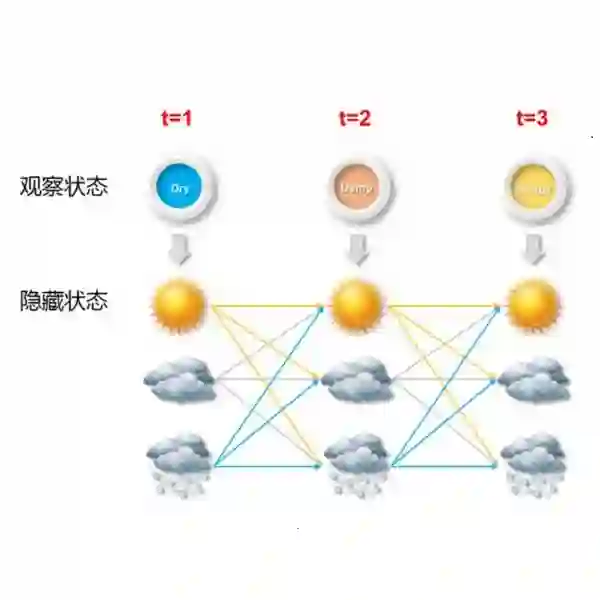
We consider inference problems for a class of continuous state collective hidden Markov models, where the data is recorded in aggregate (collective) form generated by a large population of individuals following the same dynamics. We propose an aggregate inference algorithm called collective Gaussian forward-backward algorithm, extending recently proposed Sinkhorn belief propagation algorithm to models characterized by Gaussian densities. Our algorithm enjoys convergence guarantee. In addition, it reduces to the standard Kalman filter when the observations are generated by a single individual. The efficacy of the proposed algorithm is demonstrated through multiple experiments.
翻译:我们考虑了一组连续的国家集体隐藏的Markov模型的推论问题,在这个模型中,数据以综合(集体)形式记录,由大量个人根据同样的动态生成。 我们提出了一种总推论算法,称为Gaussian 集体前向后向算法,将最近提出的Sinkhorn信仰传播算法扩展至以Gaussian密度为特征的模型。我们的算法享有趋同保证。此外,当观察由单个个人生成时,它会降低为标准的Kalman过滤法。提议的算法的效力可以通过多重实验得到证明。