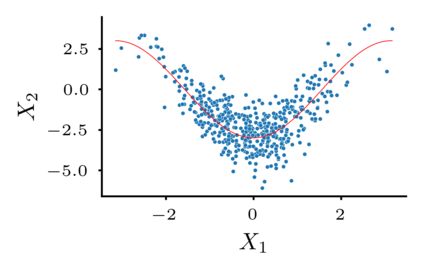
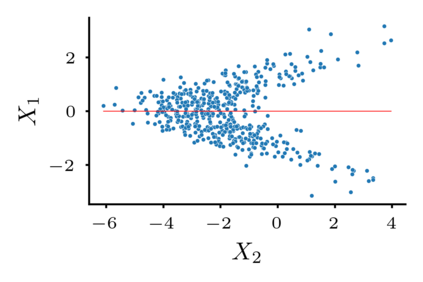
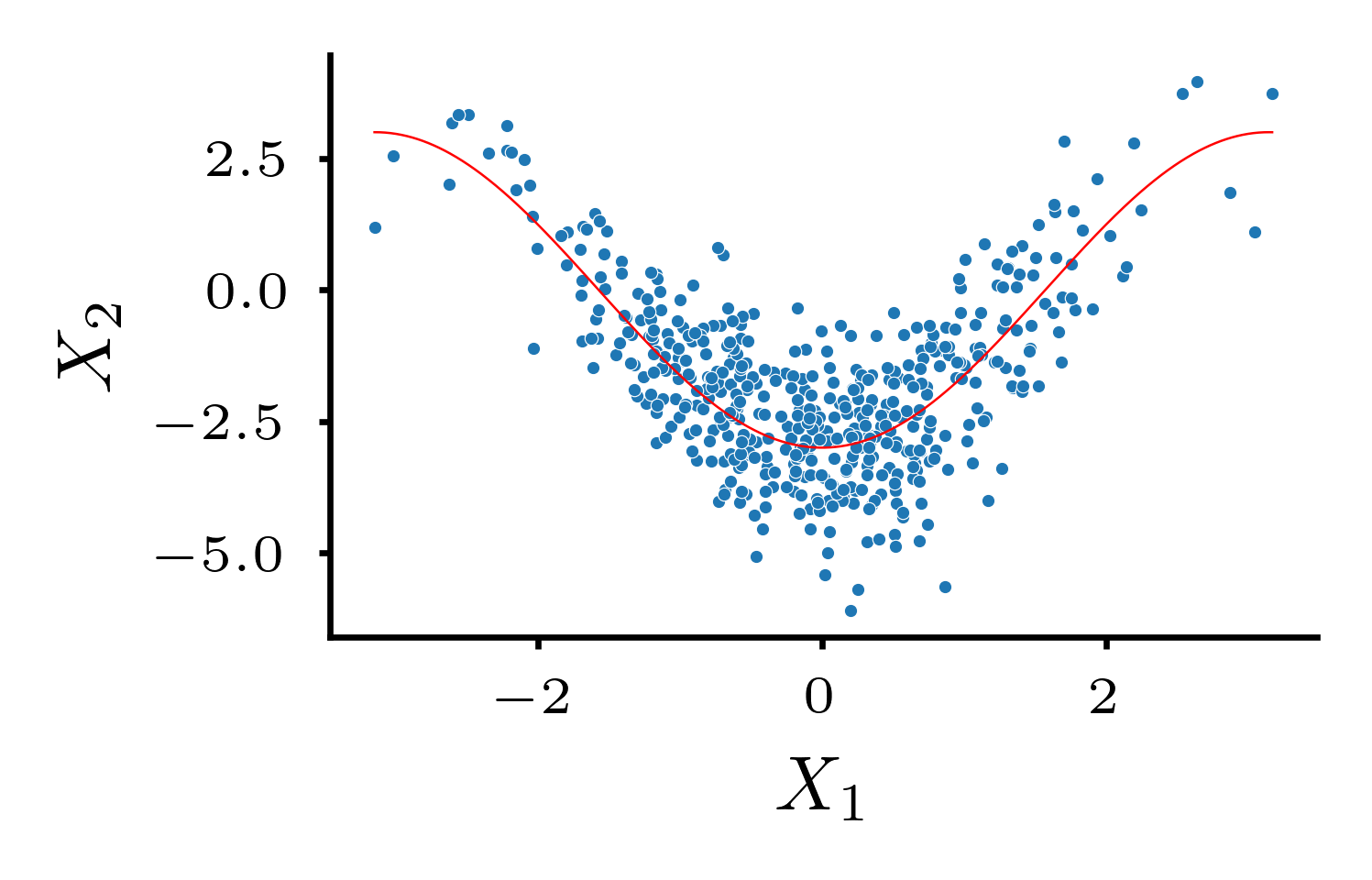
We present a boosting-based method to learn additive Structural Equation Models (SEMs) from observational data, with a focus on the theoretical aspects of determining the causal order among variables. We introduce a family of score functions based on arbitrary regression techniques, for which we establish necessary conditions to consistently favor the true causal ordering. Our analysis reveals that boosting with early stopping meets these criteria and thus offers a consistent score function for causal orderings. To address the challenges posed by high-dimensional data sets, we adapt our approach through a component-wise gradient descent in the space of additive SEMs. Our simulation study underlines our theoretical results for lower dimensions and demonstrates that our high-dimensional adaptation is competitive with state-of-the-art methods. In addition, it exhibits robustness with respect to the choice of the hyperparameters making the procedure easy to tune.
翻译:暂无翻译