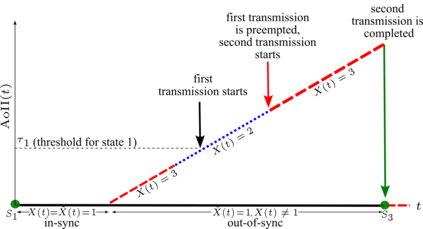
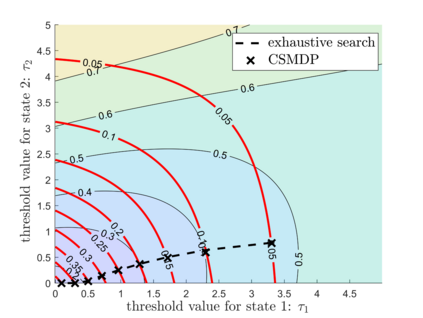
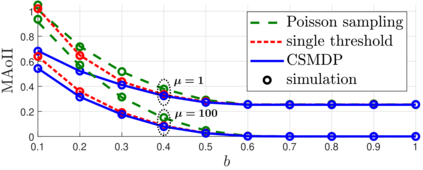
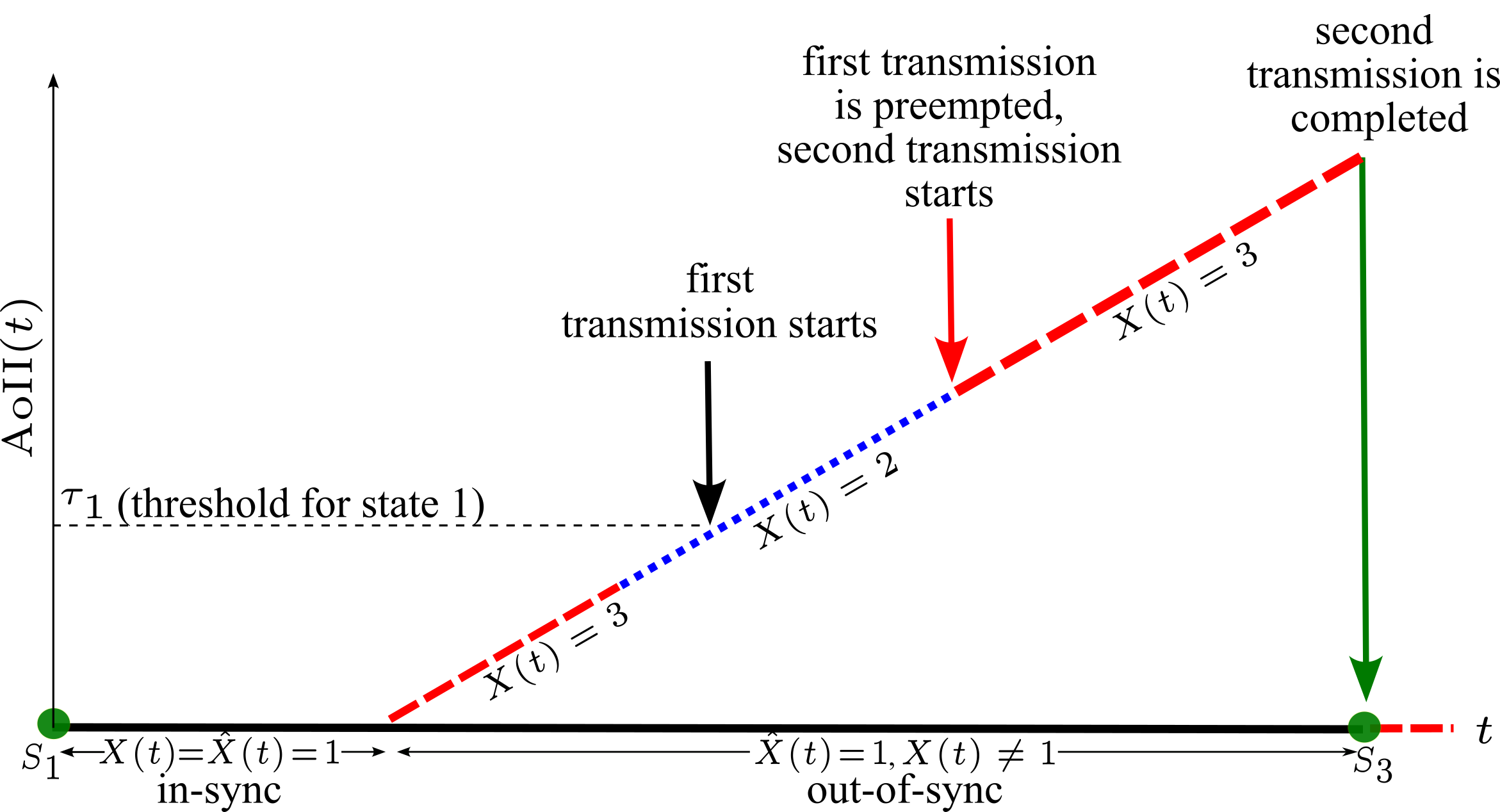
We consider a sensor that samples an $N$-state continuous-time Markov chain (CTMC)-based information source process, and transmits the observed state of the source, to a remote monitor tasked with timely tracking of the source process. The mismatch between the source and monitor processes is quantified by age of incorrect information (AoII), which penalizes the mismatch as it stays longer, and our objective is to minimize the average AoII under an average sampling rate constraint. We assume a perfect reverse channel and hence the sensor has information of the estimate while initiating a transmission or preempting an ongoing transmission. First, by modeling the problem as an average cost constrained semi-Markov decision process (CSMDP), we show that the structure of the problem gives rise to an optimum threshold policy for which the sensor initiates a transmission once the AoII exceeds a threshold depending on the instantaneous values of both the source and monitor processes. However, due to the high complexity of obtaining the optimum policy in this general setting, we consider a relaxed problem where the thresholds are allowed to be dependent only on the estimate. We show that this relaxed problem can be solved with a novel CSMDP formulation based on the theory of absorbing MCs, with a computational complexity of $\mathcal{O}(N^4)$, allowing one to obtain optimum policies for general CTMCs with over a hundred states.
翻译:暂无翻译