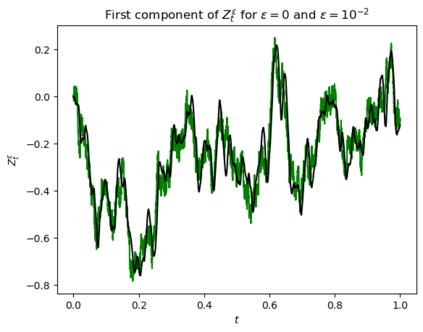
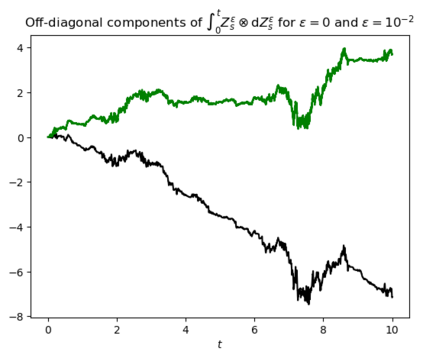
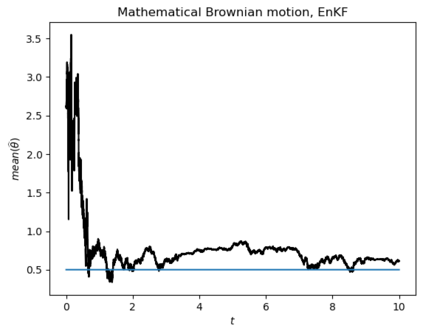
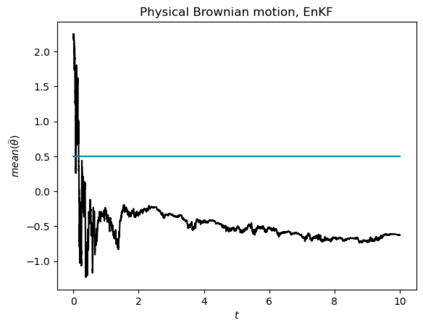
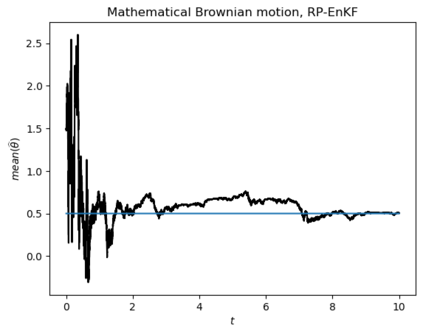
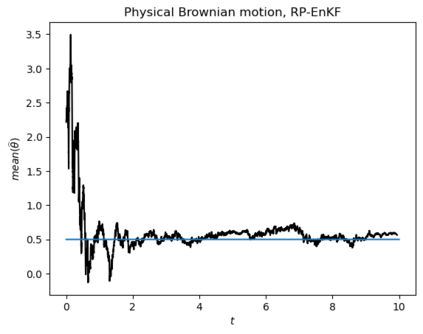
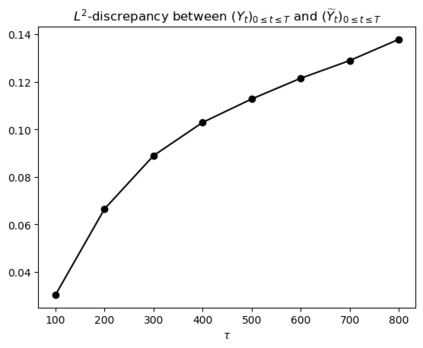
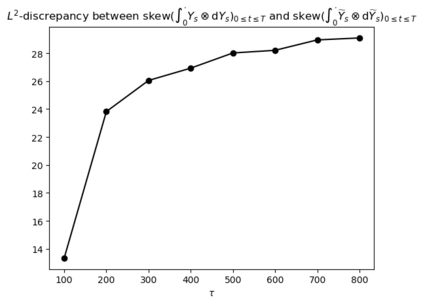
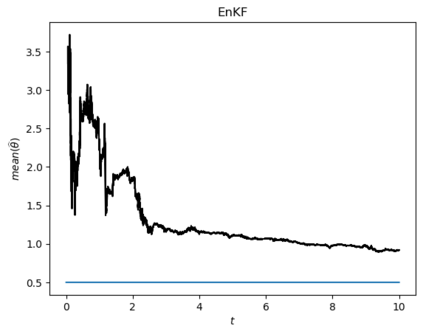
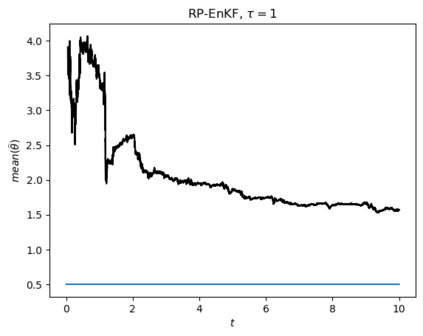
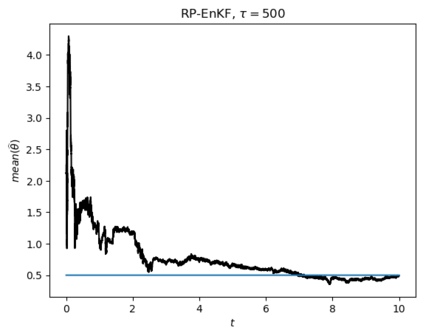
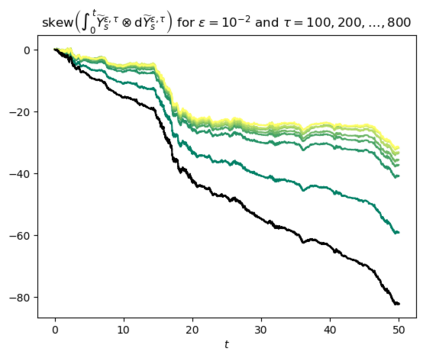
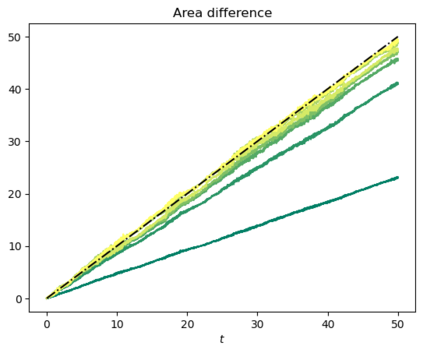
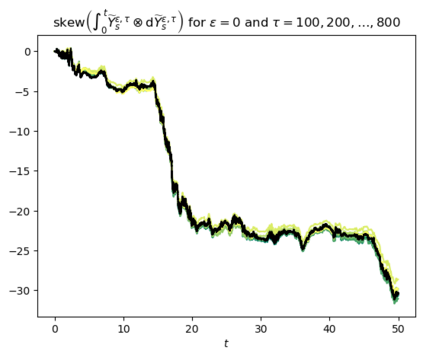
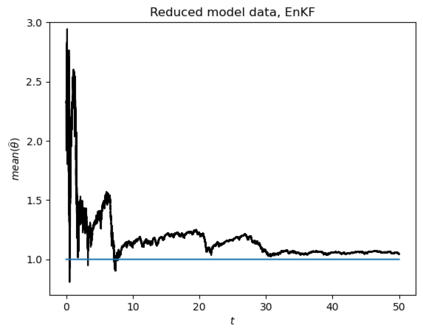
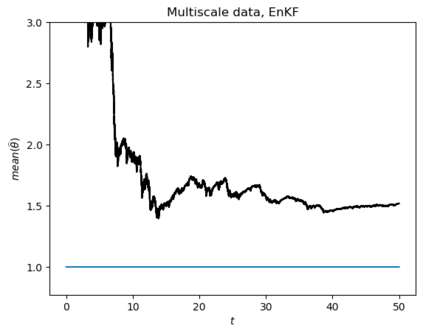
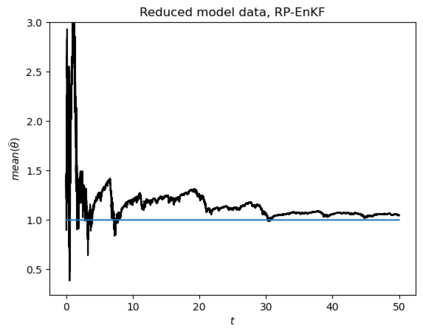
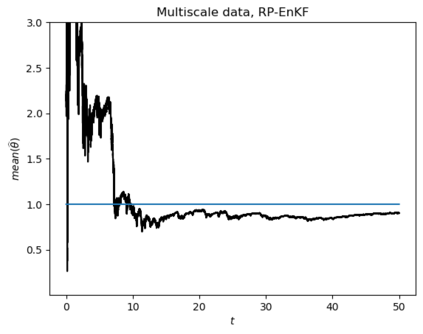
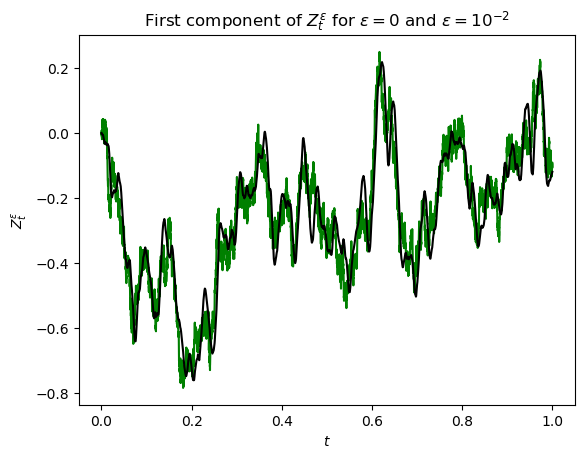
Motivated by the challenge of incorporating data into misspecified and multiscale dynamical models, we study a McKean-Vlasov equation that contains the data stream as a common driving rough path. This setting allows us to prove well-posedness as well as continuity with respect to the driver in an appropriate rough-path topology. The latter property is key in our subsequent development of a robust data assimilation methodology: We establish propagation of chaos for the associated interacting particle system, which in turn is suggestive of a numerical scheme that can be viewed as an extension of the ensemble Kalman filter to a rough-path framework. Finally, we discuss a data-driven method based on subsampling to construct suitable rough path lifts and demonstrate the robustness of our scheme in a number of numerical experiments related to parameter estimation problems in multiscale contexts.
翻译:基于将数据纳入错误指定和多尺度动态模型的挑战,我们研究了麦肯-弗拉索夫方程式,该方程式包含数据流,作为共同的粗路路径。这一方程式使我们能够在适当的粗路地形学中证明驱动器的完备性和连续性。后一种属性是我们随后制定稳健的数据同化方法的关键:我们为相关的互动粒子系统建立混乱的传播,这反过来又表明一个数字方案,可被视为将全套Kalman过滤器扩展至粗路框架。最后,我们讨论一种基于次级抽样的数据驱动方法,以构建适当的粗路升动,并表明我们在多尺度环境中与参数估计问题相关的若干数字实验中的计划是否稳健。