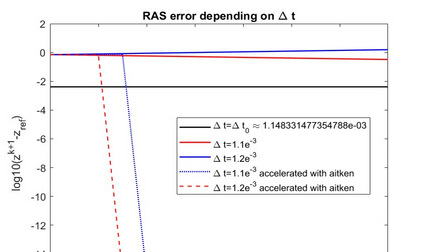
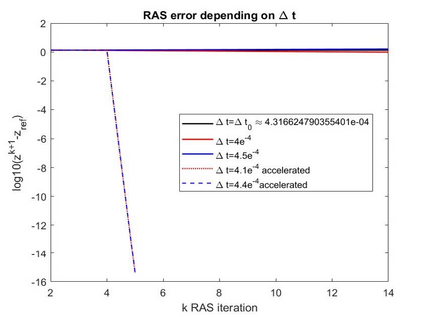
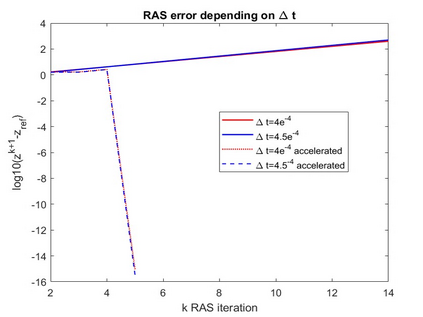
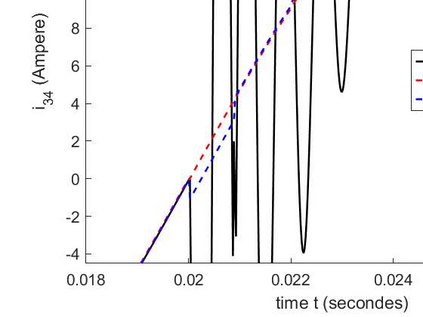
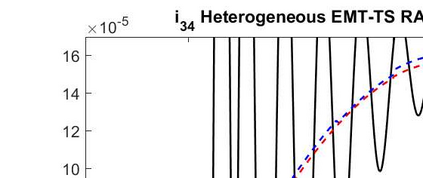
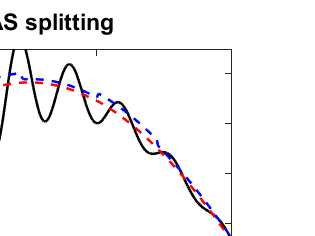
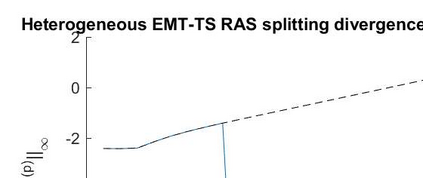
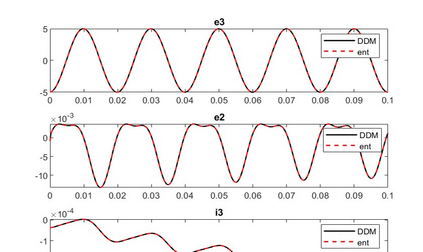
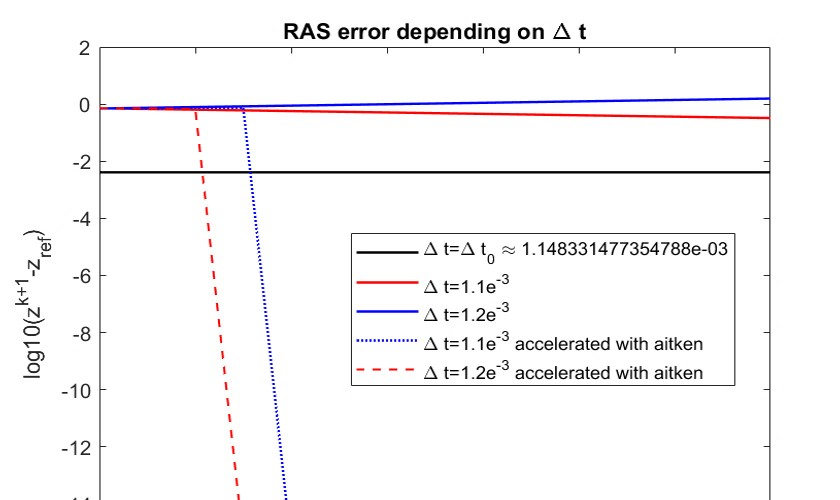
The dynamic iteration method with a restricted additive Schwarz splitting is investigated to co-simulate linear differential algebraic equations system coming from RLC electrical circuit with linear components. We show the pure linear convergence or divergence of the method with respect to the linear operator belonging to the restricted additive Schwarz interface. It allows us to accelerate it toward the true solution with the Aitken's technique for accelerating convergence. This provides a dynamic iteration method less sensitive to the splitting. Numerical examples with convergent and divergent splitting show the efficiency of the proposed approach. We also test it on a linear RLC circuit combining different types of circuit modeling (Transient Stability model and Electro-Magnetic Transient model) with overlapping partitions. Finally, some results for a weakly nonlinear differential algebraic equations system are also provided.
翻译:使用限制添加剂Schwarz分离的动态迭代法被调查,以共同模拟来自RLC电路的线性差代数方程式系统,并配有线性组件。我们展示了属于限制添加剂Schwarz界面的线性操作员使用的方法的纯线性趋同或差异。它使我们能够加速它,用Aitken的加速趋同技术找到真正的解决办法。这提供了一种对分离不那么敏感的动态迭代法。聚合和分裂的数值示例显示了拟议方法的效率。我们还在一种线性RLC电路线路上测试它,将不同类型的电路建模(中度稳定模型和电磁中转模型)与重叠的分区结合起来。最后,还提供了微弱的非线性差代数方程式系统的一些结果。