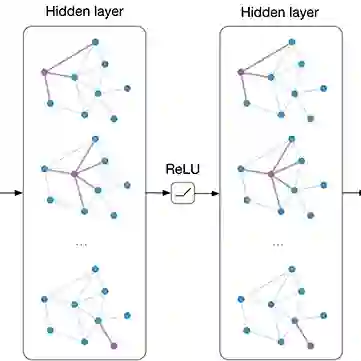
Graph Convolutional Network (GCN) with the powerful capacity to explore graph-structural data has gained noticeable success in recent years. Nonetheless, most of the existing GCN-based models suffer from the notorious over-smoothing issue, owing to which shallow networks are extensively adopted. This may be problematic for complex graph datasets because a deeper GCN should be beneficial to propagating information across remote neighbors. Recent works have devoted effort to addressing over-smoothing problems, including establishing residual connection structure or fusing predictions from multi-layer models. Because of the indistinguishable embeddings from deep layers, it is reasonable to generate more reliable predictions before conducting the combination of outputs from various layers. In light of this, we propose an Alternating Graph-regularized Neural Network (AGNN) composed of Graph Convolutional Layer (GCL) and Graph Embedding Layer (GEL). GEL is derived from the graph-regularized optimization containing Laplacian embedding term, which can alleviate the over-smoothing problem by periodic projection from the low-order feature space onto the high-order space. With more distinguishable features of distinct layers, an improved Adaboost strategy is utilized to aggregate outputs from each layer, which explores integrated embeddings of multi-hop neighbors. The proposed model is evaluated via a large number of experiments including performance comparison with some multi-layer or multi-order graph neural networks, which reveals the superior performance improvement of AGNN compared with state-of-the-art models.
翻译:图卷积网络(GCN)因其探索图形结构化数据的强大能力而在近年来取得了显著的成功。然而,大多数现有的基于GCN的模型都面临着臭名昭著的过度平滑问题,因此广泛采用浅层网络。这对于复杂的图形数据集可能是有问题的,因为更深层的GCN应该有利于在远距离邻居之间传播信息。最近的工作致力于解决过度平滑问题,包括建立残差连接结构或融合来自多层模型的预测。由于深层中无法区分的嵌入,因此在进行来自各个层的输出的组合之前生成更可靠的预测是合理的。基于此,我们提出了一个交替图-正则化神经网络(AGNN),由图卷积层(GCL)和图嵌入层(GEL)组成。GEL源自包含拉普拉斯嵌入项的图正则化优化,它可以通过从低阶特征空间向高阶空间的定期投影来缓解过度平滑问题。使用具有更加可辨识的不同层特征的改进的Adaboost策略来聚合每个层的输出,该策略探索了多跳邻居的综合嵌入。该模型通过大量的实验进行评估,包括与一些多层或多阶图神经网络的性能比较,这揭示了AGNN相对于最先进模型的优越性能改进。