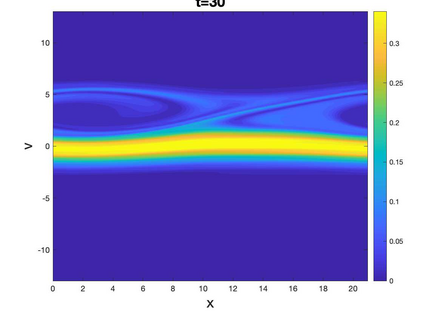
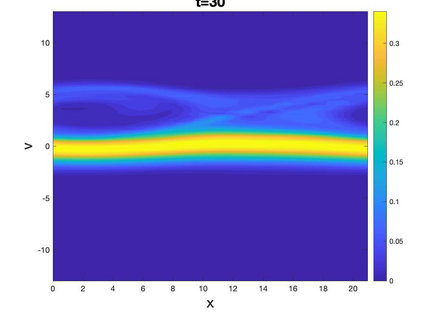
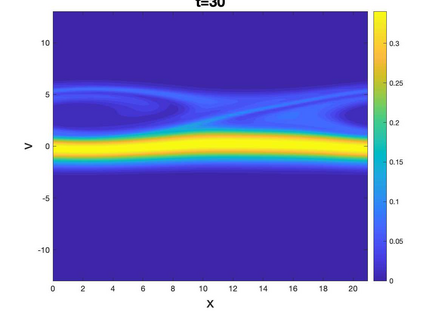
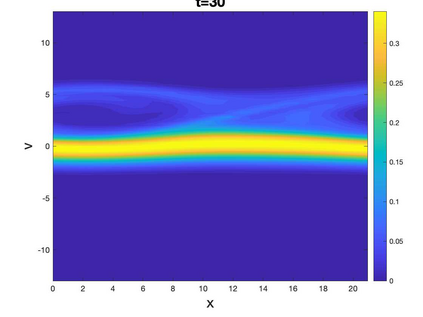
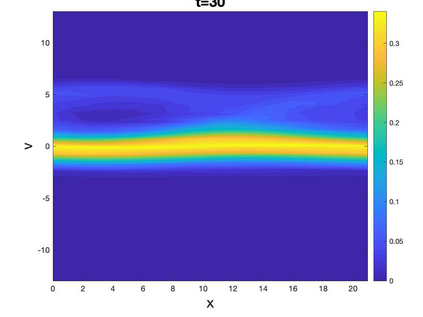
In this paper, we propose a novel Local Macroscopic Conservative (LoMaC) low rank tensor method with discontinuous Galerkin (DG) discretization for the physical and phase spaces for simulating the Vlasov-Poisson (VP) system. The LoMaC property refers to the exact local conservation of macroscopic mass, momentum and energy at the discrete level. The recently developed LoMaC low rank tensor algorithm (arXiv:2207.00518) simultaneously evolves the macroscopic conservation laws of mass, momentum and energy using the kinetic flux vector splitting; then the LoMaC property is realized by projecting the low rank kinetic solution onto a subspace that shares the same macroscopic observables. This paper is a generalization of our previous work, but with DG discretization to take advantage of its compactness and flexibility in handling boundary conditions and its superior accuracy in the long term. The algorithm is developed in a similar fashion as that for a finite difference scheme, by observing that the DG method can be viewed equivalently in a nodal fashion. With the nodal DG method, assuming a tensorized computational grid, one will be able to (1) derive differentiation matrices for different nodal points based on a DG upwind discretization of transport terms, and (2) define a weighted inner product space based on the nodal DG grid points. The algorithm can be extended to the high dimensional problems by hierarchical Tucker decomposition of solution tensors and a corresponding conservative projection algorithm. In a similar spirit, the algorithm can be extended to DG methods on nodal points of an unstructured mesh, or to other types of discretization, e.g. the spectral method in velocity direction. Extensive numerical results are performed to showcase the efficacy of the method.
翻译:在本文中, 我们提出一种新的本地宏观保守( LoMaC) 低等级调高( LoMac) 方法, 使用不连续的 Galerkin (DG), 用于模拟 Vlasov- Poisson (VP) 系统的物理和阶段空间分解。 LoMaC 属性指的是在离异级别上对宏观质量、 动力和能量进行精确的本地保护。 最近开发的 LoMaC 低等级 Exmor 算法( arXiv: 2207. 00518) 的同时, 利用动态通量矢量矢量分解分解, 使质量、 动力和能量的宏观保护法; 然后, 将低等级的动态解压法分解为分解( DG), 将低等级的动力化法分解( DG ) 推向一个分解( DG), 以不连续的递解( DG) 方法向上, 将一个不连续的递解( DG) 数据解( DG) 以不易变的变压方法进行。