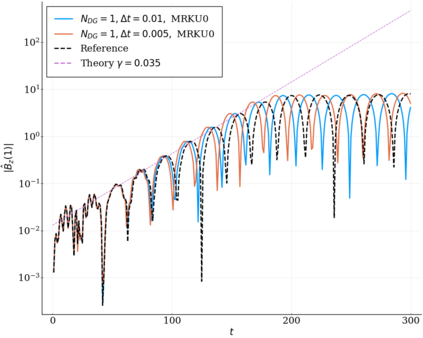
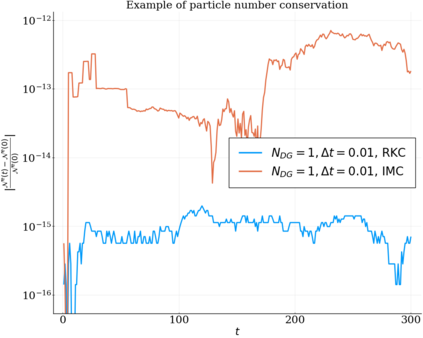
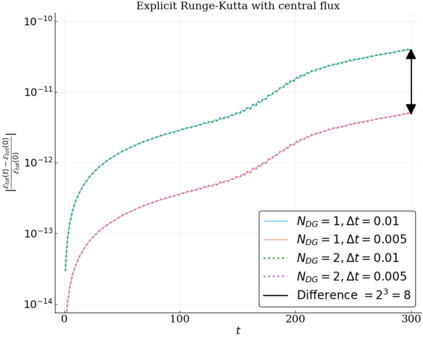
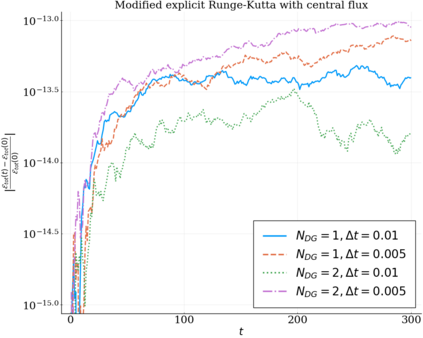
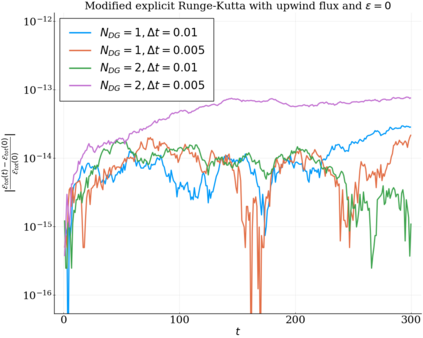
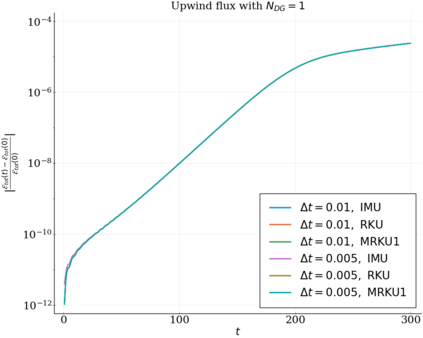
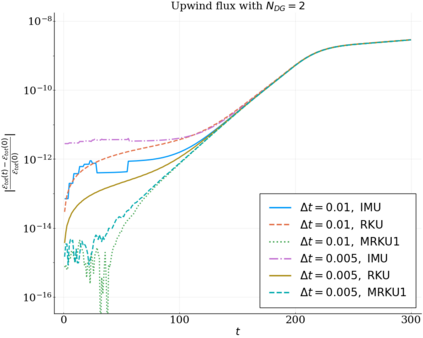
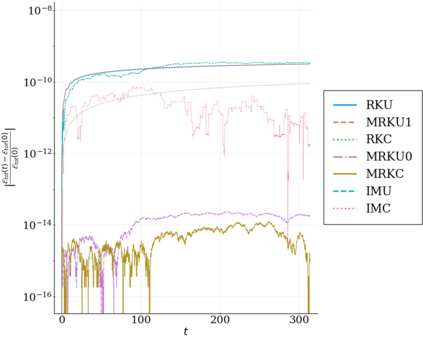
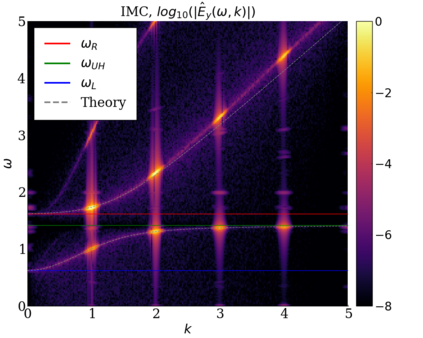
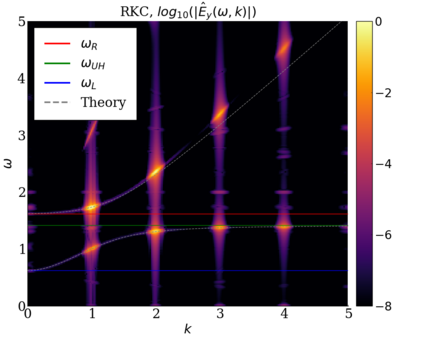
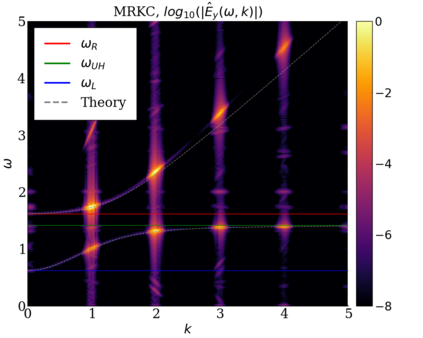
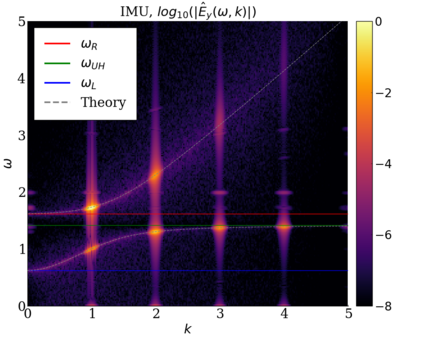
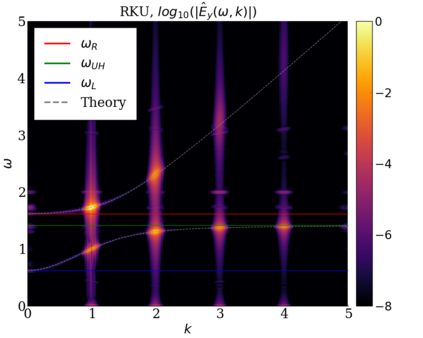
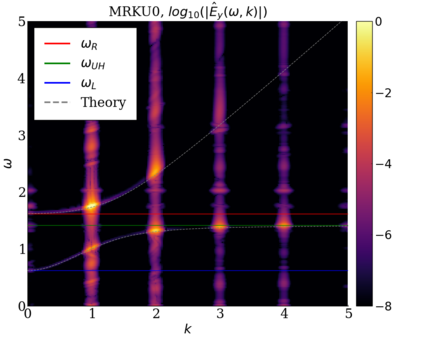
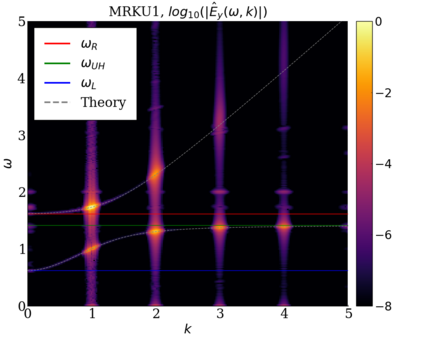
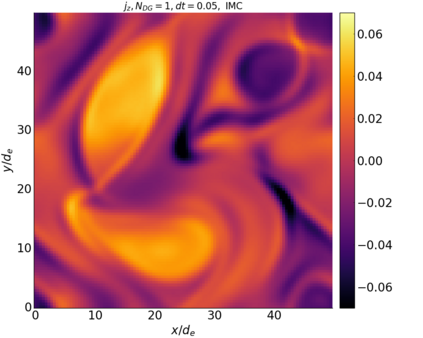
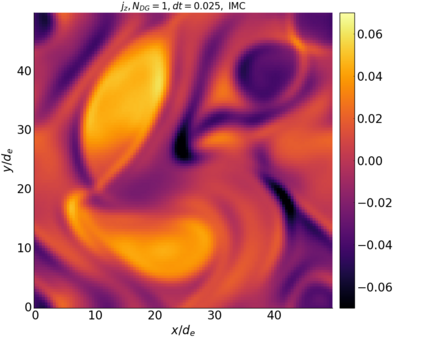
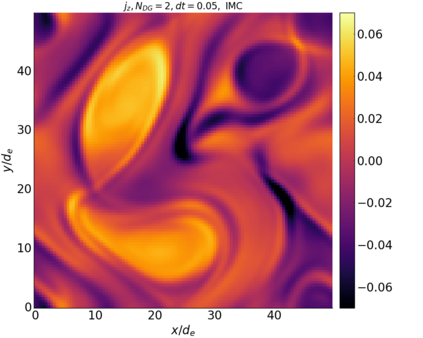
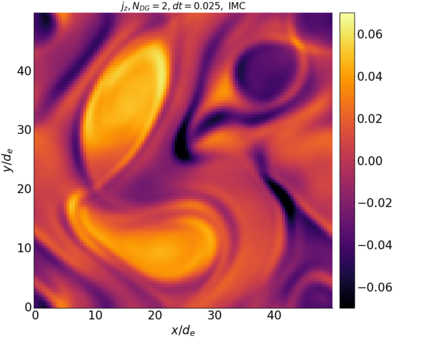
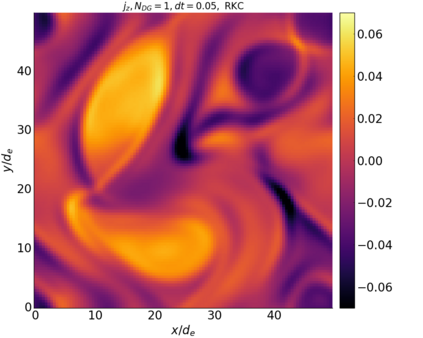
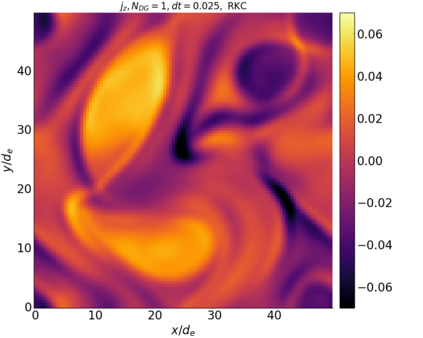
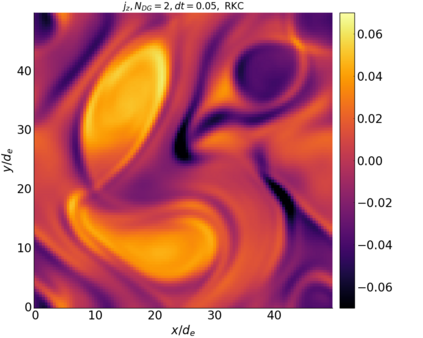
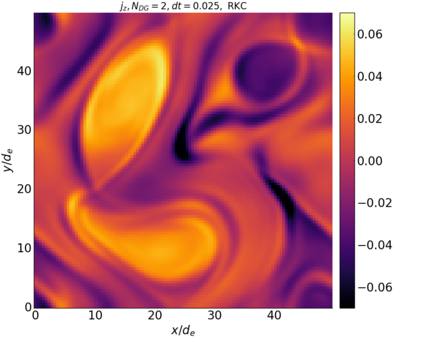
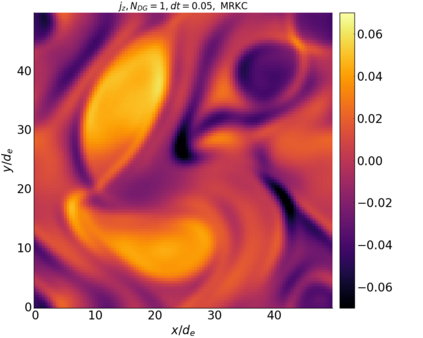
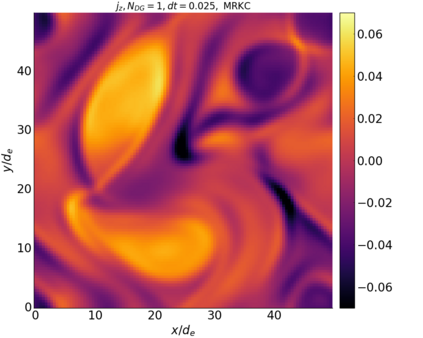
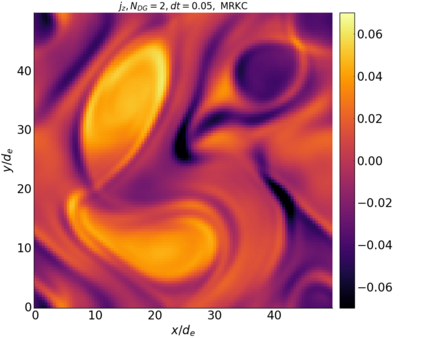
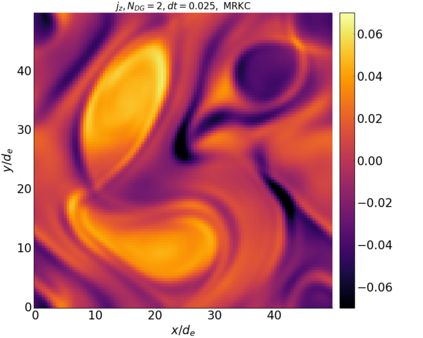
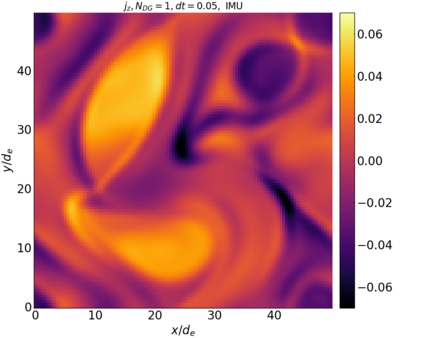
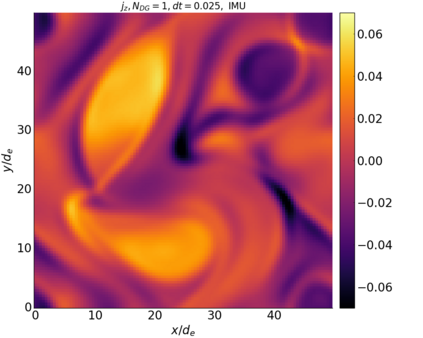
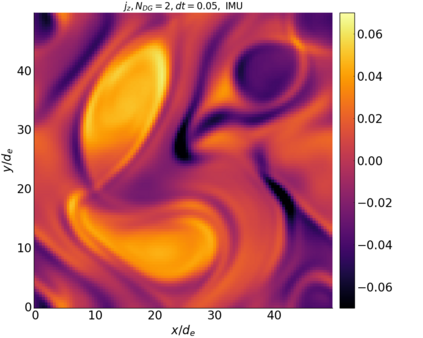
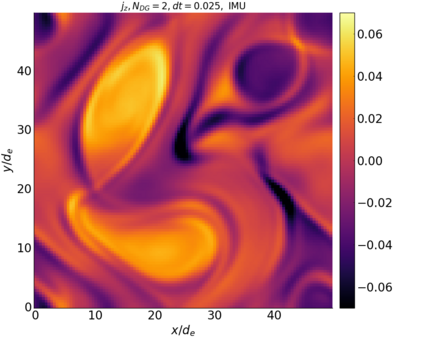
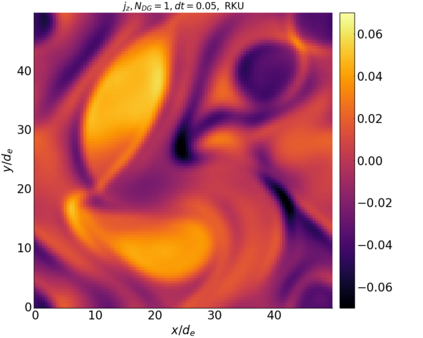
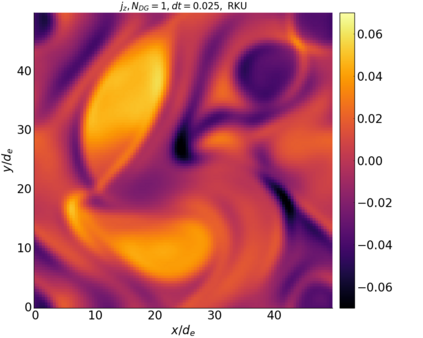
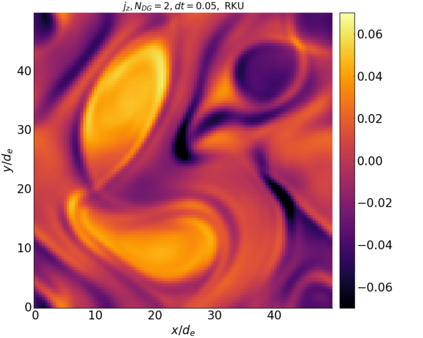
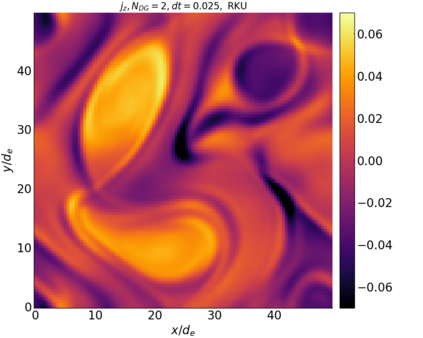
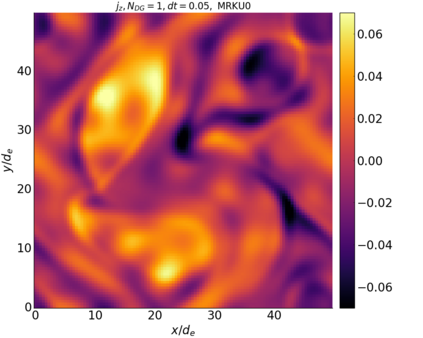
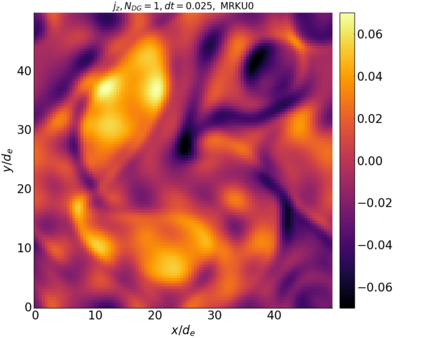
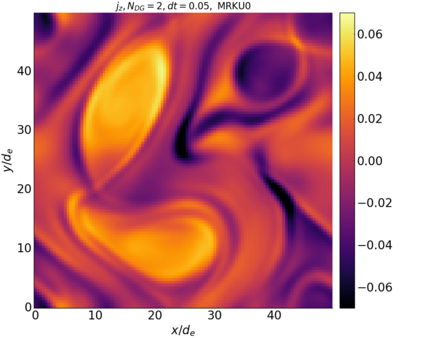
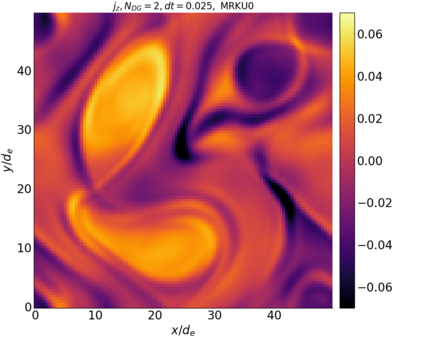
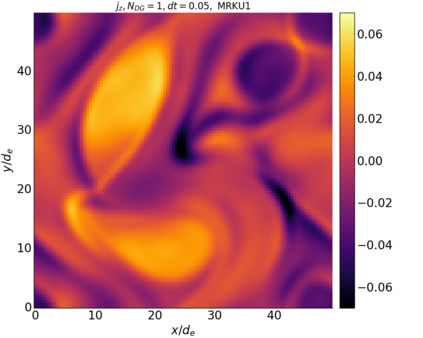
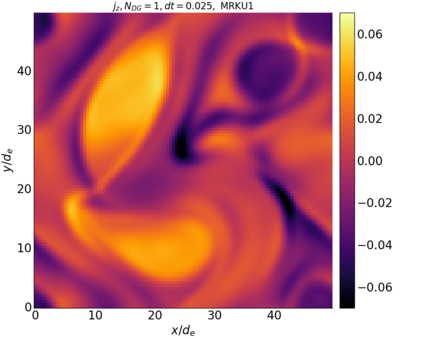
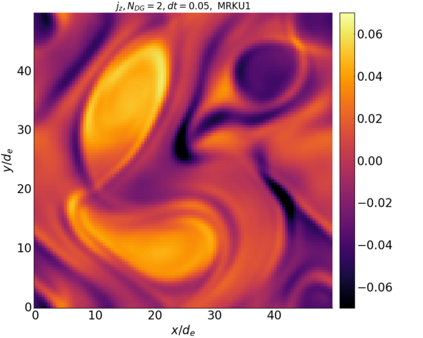
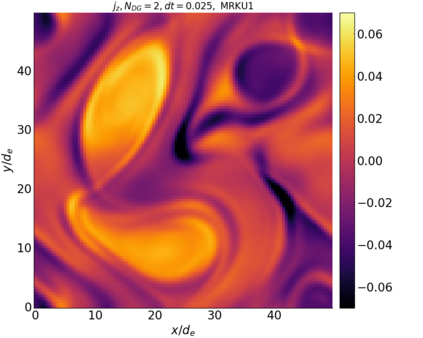
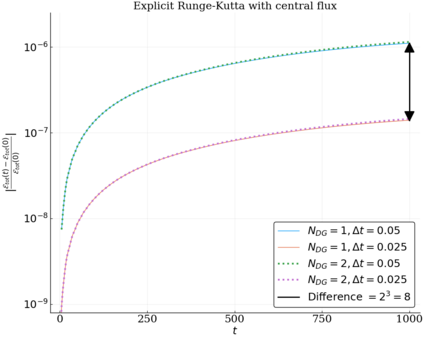
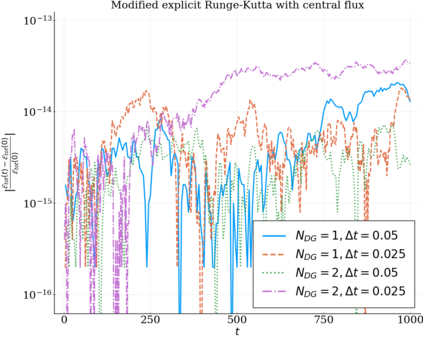
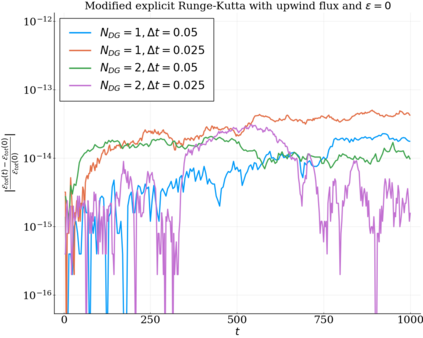
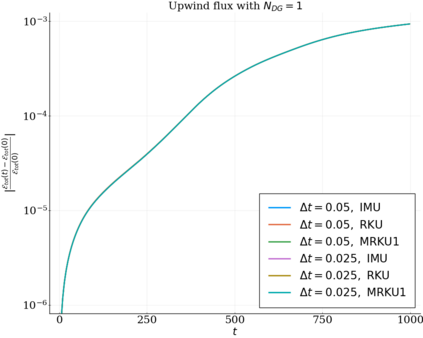
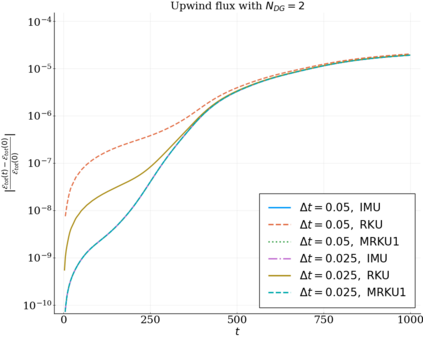
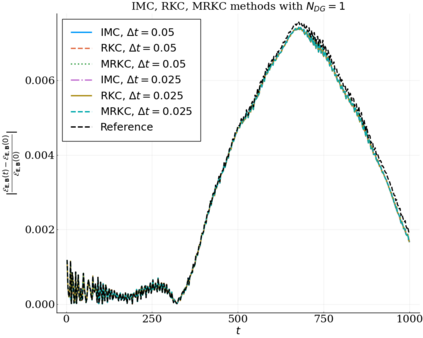
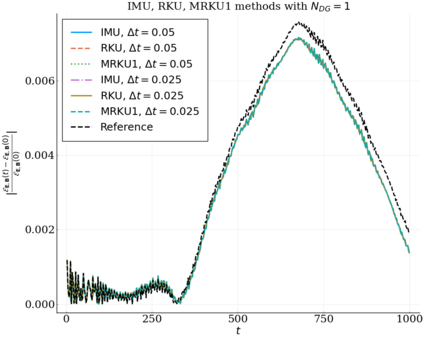
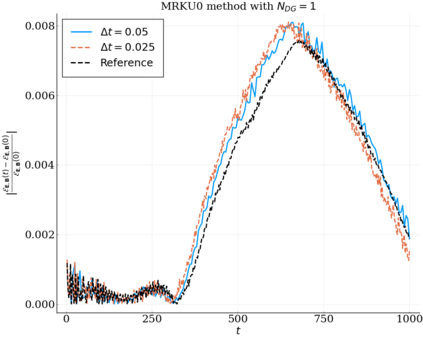
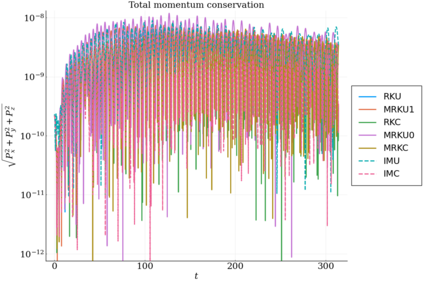
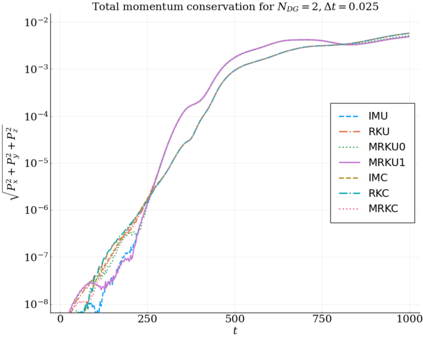
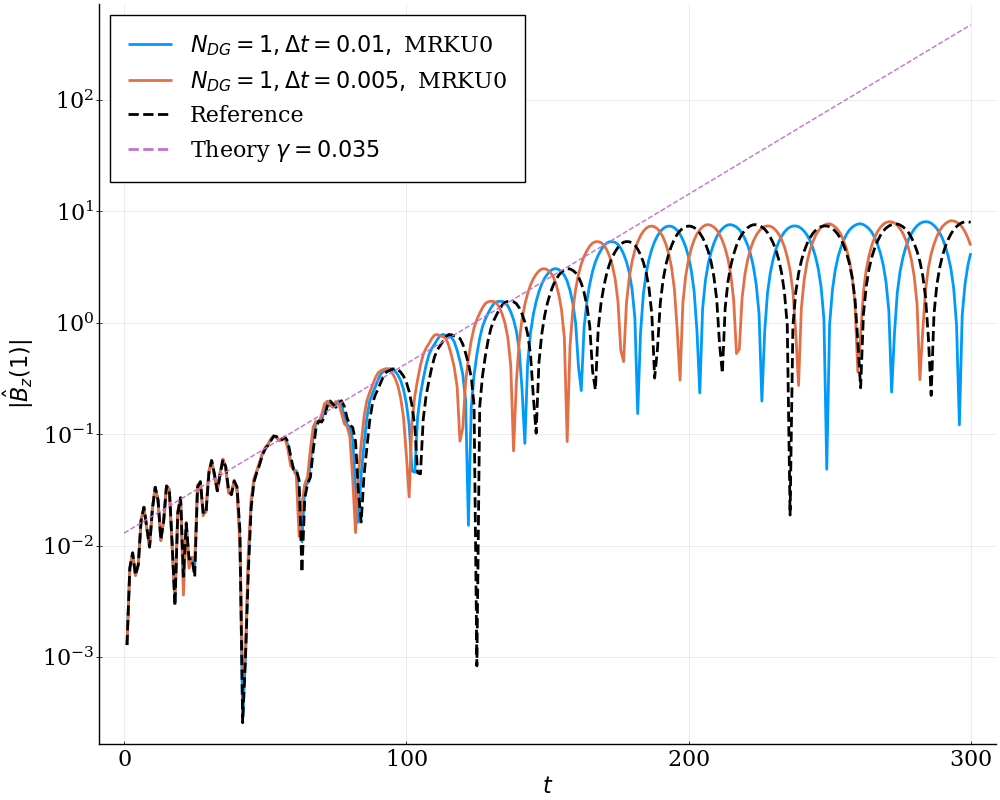
We study the conservation properties of the Hermite-discontinuous Galerkin (Hermite-DG) approximation of the Vlasov-Maxwell equations. In this semi-discrete formulation, the total mass is preserved independently for every plasma species. Further, an energy invariant exists if central numerical fluxes are used in the DG approximation of Maxwell's equations, while a dissipative term is present when upwind fluxes are employed. In general, traditional temporal integrators might fail to preserve invariants associated with conservation laws during the time evolution. Hence, we analyze the capability of explicit and implicit Runge-Kutta (RK) temporal integrators to preserve such invariants. Since explicit RK methods can only ensure preservation of linear invariants but do not provide any control on the system energy, we consider modified explicit RK methods in the family of relaxation Runge-Kutta methods (RRK). These methods can be tuned to preserve the energy invariant at the continuous or semi-discrete level, a distinction that is important when upwind fluxes are used in the discretization of Maxwell's equations since upwind provides a numerical source of energy dissipation that is not present when central fluxes are used. We prove that the proposed methods are able to preserve the energy invariant and to maintain the semi-discrete energy dissipation (if present) according to the discretization of Maxwell's equations. An extensive set of numerical experiments corroborates the theoretical findings. It also suggests that maintaining the semi-discrete energy dissipation when upwind fluxes are used leads to an overall better accuracy of the method relative to using upwind fluxes while forcing exact energy conservation.
翻译:我们研究的是Vlasov-Maxwell 方程式的赫尔米特不连续的Galerkin(Hermite-DG)近似离差(Hermite-DG)的保存特性。 在这种半分解配方中,总质量被独立保存在每个等离子物种中。 此外,如果在最大韦尔方程式的DG近差中使用中央数字通量,而当使用顺风通量时,则会出现一个消散的术语。一般而言,传统的时空集成体可能无法保存与时间演变过程中的节能法相关的变异体。因此,我们分析了内向和内隐含的Runge-Kutta(RKK)时间融合器的总质量,以保持这些变异异性。在使用离子变异变法时,当使用离子变异体法时,这种变异性变异体的变异性将变得很重要。 当使用离子变异法时,当我们使用离子变异的能量变异法时,这种变异性变异的变变变异法会显示我们使用的动力变异的变异的变异的方法是使用。