Statistical methods used to combine the effective reproduction number, R(t), and other related measures of COVID-19 in the UK

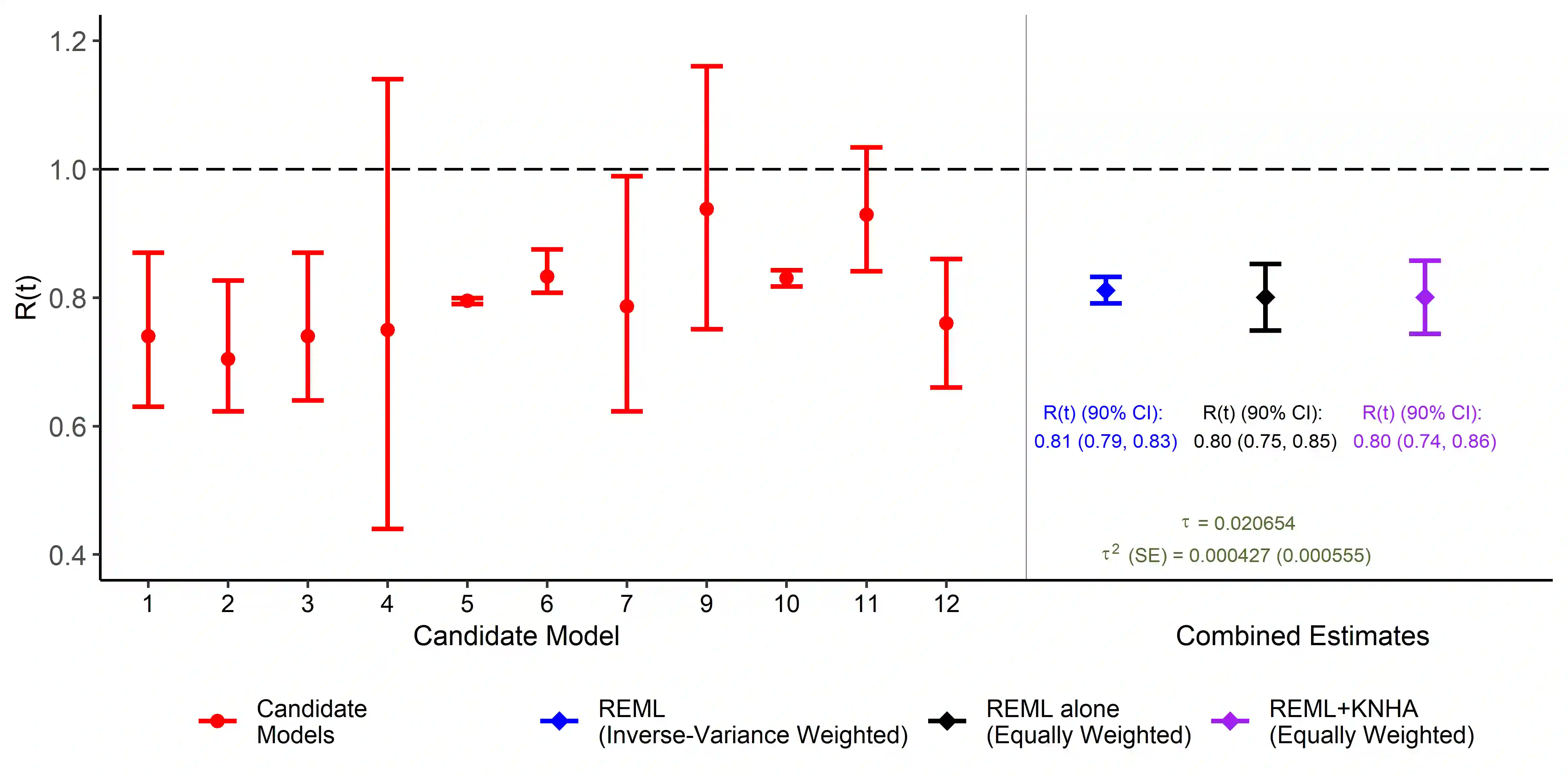
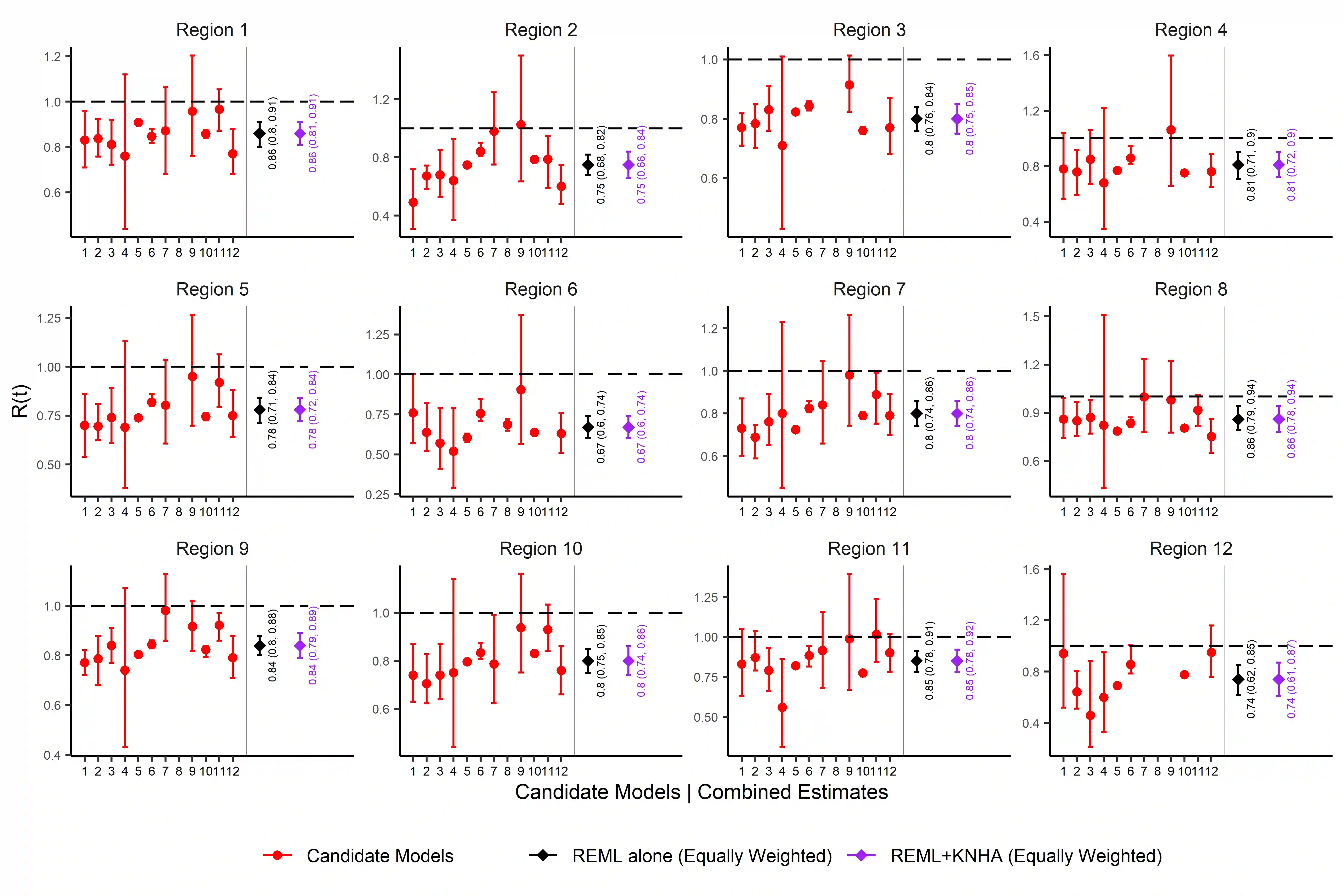
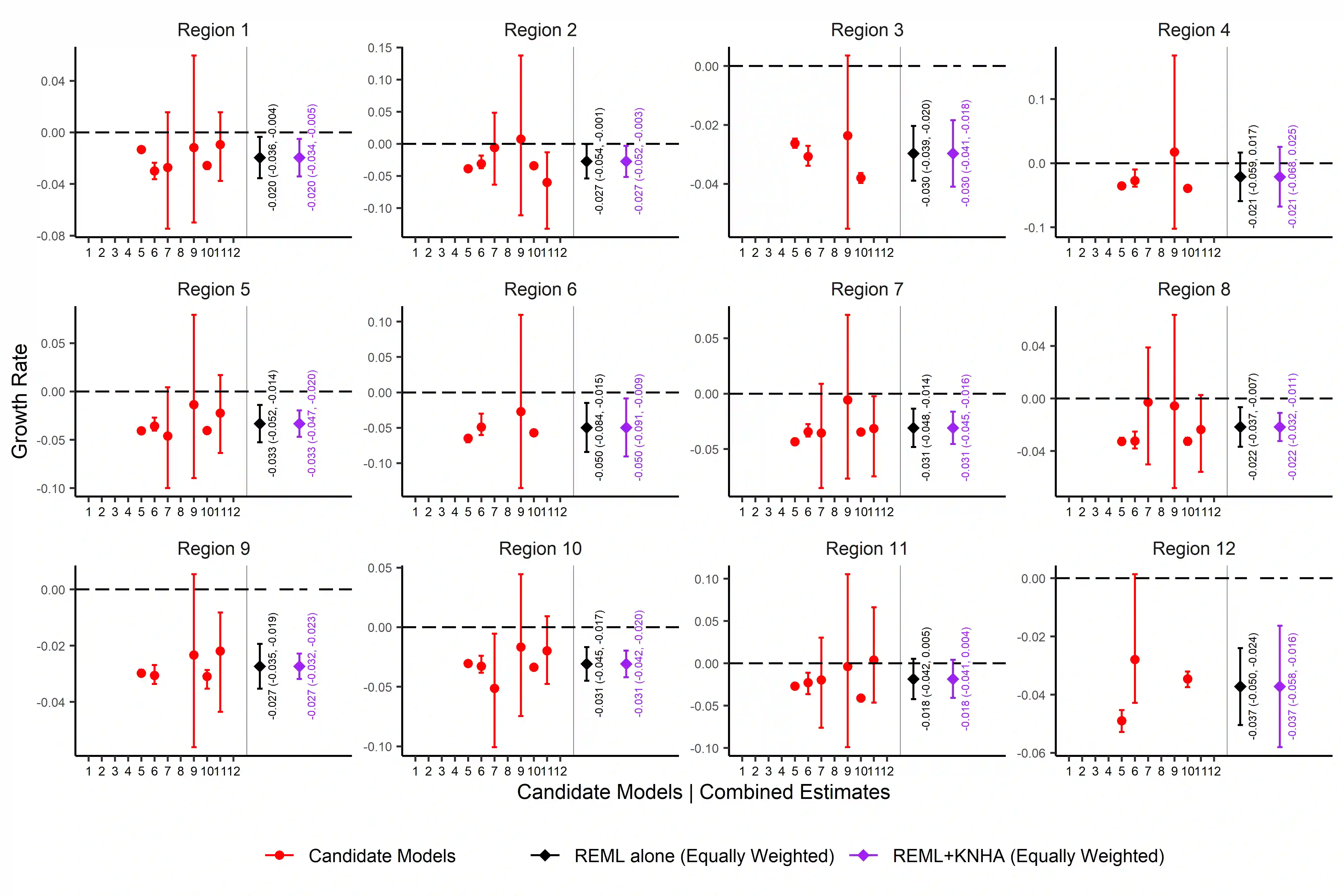
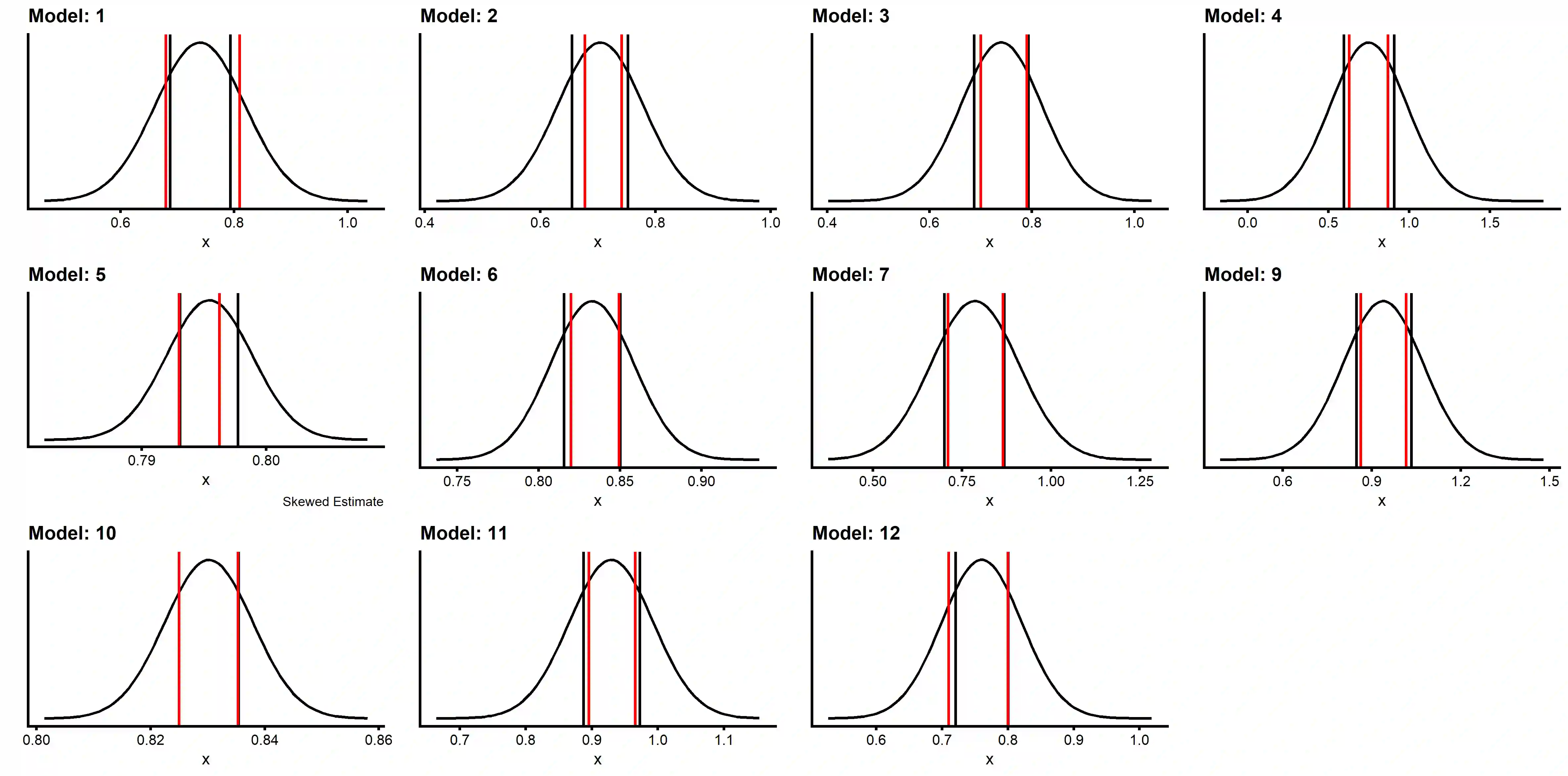
In the recent COVID-19 pandemic, a wide range of epidemiological modelling approaches have been used to predict the effective reproduction number, R(t), and other COVID-19 related measures such as the daily rate of exponential growth, r(t). These candidate models use different modelling approaches or differing assumptions about spatial or age mixing, and some capture genuine uncertainty in scientific understanding of disease dynamics. Combining estimates using appropriate statistical methodology from multiple candidate models is important to better understand the variation of these outcome measures to help inform decision making. In this paper, we combine these estimates for specific UK nations and regions using random effects meta analyses techniques, utilising the restricted maximum likelihood (REML) method to estimate the heterogeneity variance parameter, and two approaches to calculate the confidence interval for the combined estimate: the standard Wald-type intervals; and the Knapp and Hartung (KNHA) method. As estimates in this setting are derived using model predictions, each with varying degrees of uncertainty, equal weighting is favoured over the more standard inverse-variance weighting in order avoid potential up-weighting of models providing estimates with lower levels of uncertainty that are not fully accounting for inherent uncertainties. Utilising these meta-analysis techniques has allowed for statistically robust combined estimates to be calculated for key COVID-19 outcome measures. This in turn allows timely and informed decision making based on all of the available information.